辽宁省大连市真金教育信息咨询有限公司高三数学 第06章 不等式精炼试题 新人教A版 VIP免费

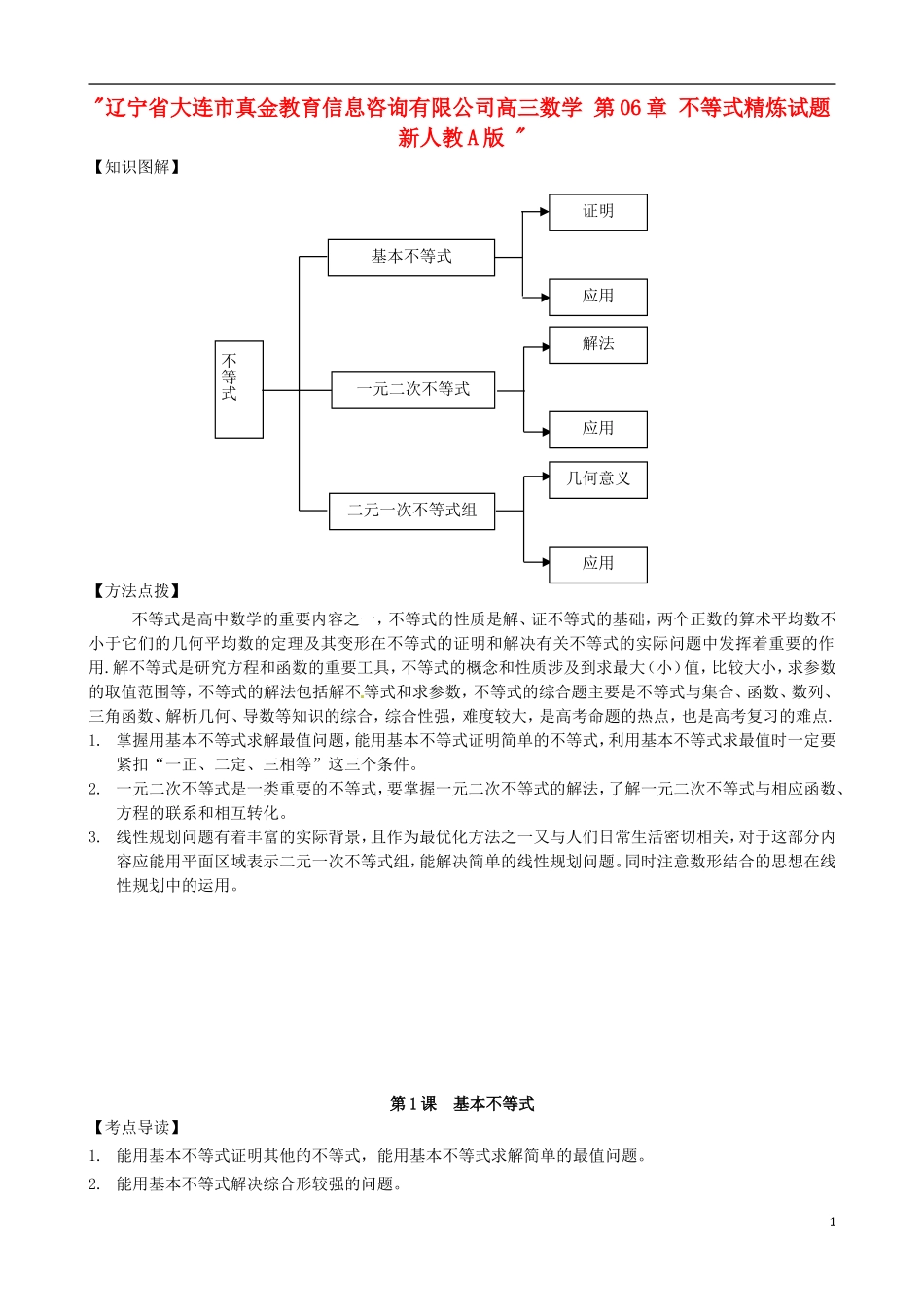
"辽宁省大连市真金教育信息咨询有限公司高三数学第06章不等式精炼试题新人教A版"【知识图解】【方法点拨】不等式是高中数学的重要内容之一，不等式的性质是解、证不等式的基础，两个正数的算术平均数不小于它们的几何平均数的定理及其变形在不等式的证明和解决有关不等式的实际问题中发挥着重要的作用.解不等式是研究方程和函数的重要工具，不等式的概念和性质涉及到求最大（小）值，比较大小，求参数的取值范围等，不等式的解法包括解不等式和求参数，不等式的综合题主要是不等式与集合、函数、数列、三角函数、解析几何、导数等知识的综合，综合性强，难度较大，是高考命题的热点，也是高考复习的难点.1.掌握用基本不等式求解最值问题，能用基本不等式证明简单的不等式，利用基本不等式求最值时一定要紧扣“一正、二定、三相等”这三个条件。2.一元二次不等式是一类重要的不等式，要掌握一元二次不等式的解法，了解一元二次不等式与相应函数、方程的联系和相互转化。3.线性规划问题有着丰富的实际背景，且作为最优化方法之一又与人们日常生活密切相关，对于这部分内容应能用平面区域表示二元一次不等式组，能解决简单的线性规划问题。同时注意数形结合的思想在线性规划中的运用。第1课基本不等式【考点导读】1.能用基本不等式证明其他的不等式，能用基本不等式求解简单的最值问题。2.能用基本不等式解决综合形较强的问题。1不等式一元二次不等式基本不等式二元一次不等式组应用解法应用几何意义应用证明【基础练习】1.“a>b>0”是“ab<222ab”的充分而不必要条件(填写充分而不必要条件、必要而不充分条件、充分必要条件、既不充分也不必要条件)2.cabcabaccbba则,2,2,1222222的最小值为1323.已知,xyR，且41xy，则xy的最大值为1614.已知lglg1xy，则52xy的最小值是2【范例导析】例1.已知54x，求函数14245yxx的最大值.分析：由于450x，所以首先要调整符号.解： 54x∴540x∴y=4x-2+145x=154354xx≤-2+3=1当且仅当15454xx，即x=1时，上式成立，故当x=1时，max1y.例2.（1）已知a，b为正常数，x、y为正实数，且1ab+=xy，求x+y的最小值。（2）已知00yx，，且302xyyx，求xy的最大值．分析：问题（1）可以采用常数代换的方法也可以进行变量代换从而转化为一元函数再利用基本不等式求解；问题（2）既可以直接利用基本不等式将题目中的等式转化为关于xy的不等式，也可以采用变量代换转换为一元函数再求解.解:(1)法一：直接利用基本不等式：abbxayx+y=(x+y)(+)=a+b++xyyx≥a+b+2ab当且仅当aybx=xyab+=1xy，即x=a+aby=b+ab时等号成立法二：由ab+=1xy得ayx=y-b2（2）法一：由302xyyx，可得，)300(230xxxy．xxxxxxxy264)2(34)2(23022264)2(34xx注意到16264)2(2264)2(xxxx．可得，18xy．当且仅当2642xx，即6x时等号成立，代入302xyyx中得3y，故xy的最大值为18．法二：Ryx,，xyxyyx22222，代入302xyyx中得：3022xyxy解此不等式得180xy．下面解法见解法一，下略．点拨：求条件最值的问题，基本思想是借助条件化二元函数为一元函数，代入法是最基本的方法，也可考虑通过变形直接利用基本不等式解决.【反馈练习】1.设a＞1,且2log(1),log(1),log(2)aaamanapa,则pnm,,的大小关系为m＞p＞n2.已知下列四个结论：①若,,Rba则22baabbaab；②若Ryx,,则yxyxlglg2lglg；③若,Rx则4424xxxx；④若,Rx则222222xxxx。其中正确的是④3.已知不等式1()()9axyxy对任意正实数,xy恒成立，则正实数a的最小值为64.（1）已知：0xy，且：1xy，求证：2222yxyx，并且求等号成立的条件．3（2）设实数x，y满足y+x2=0，0