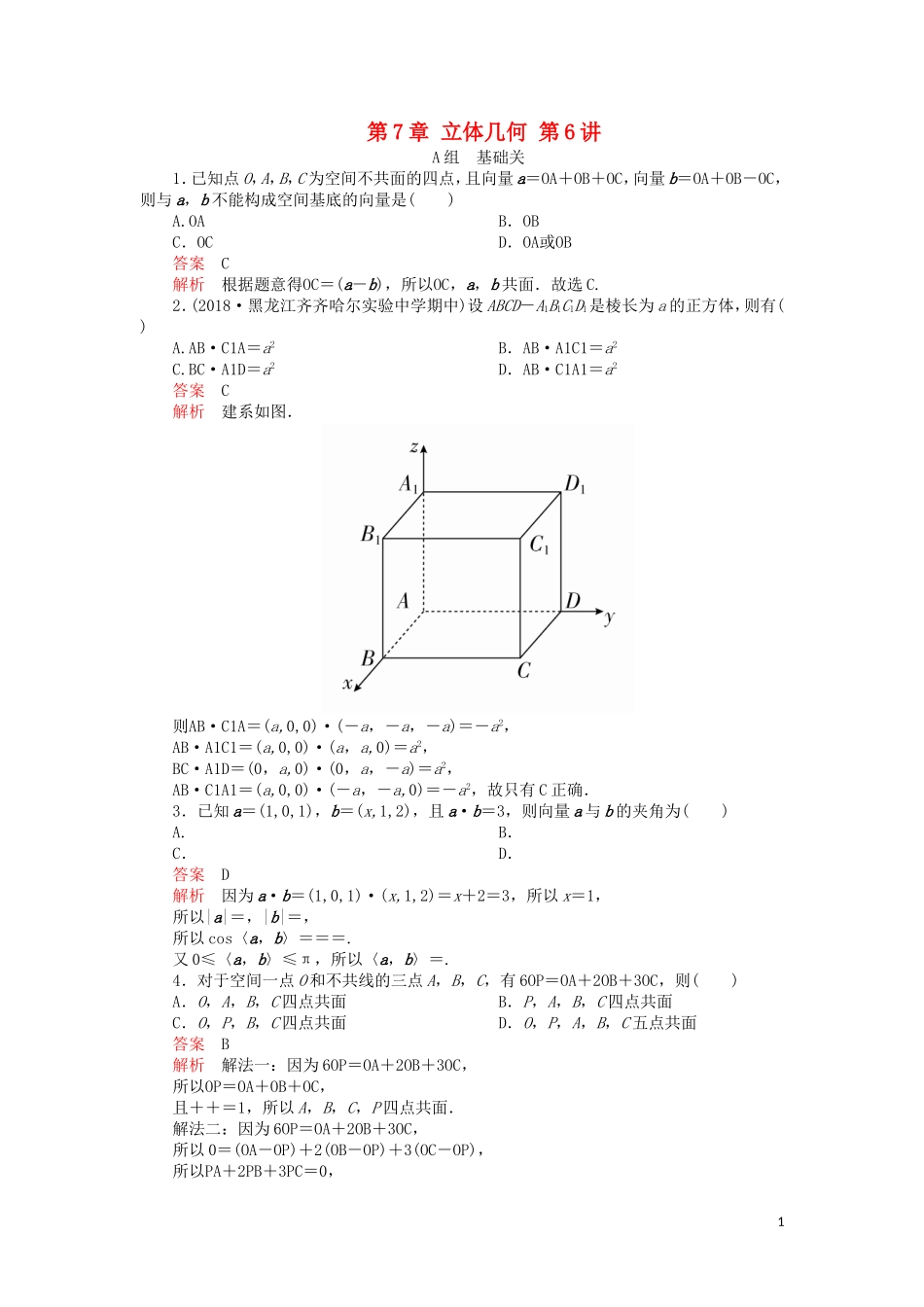
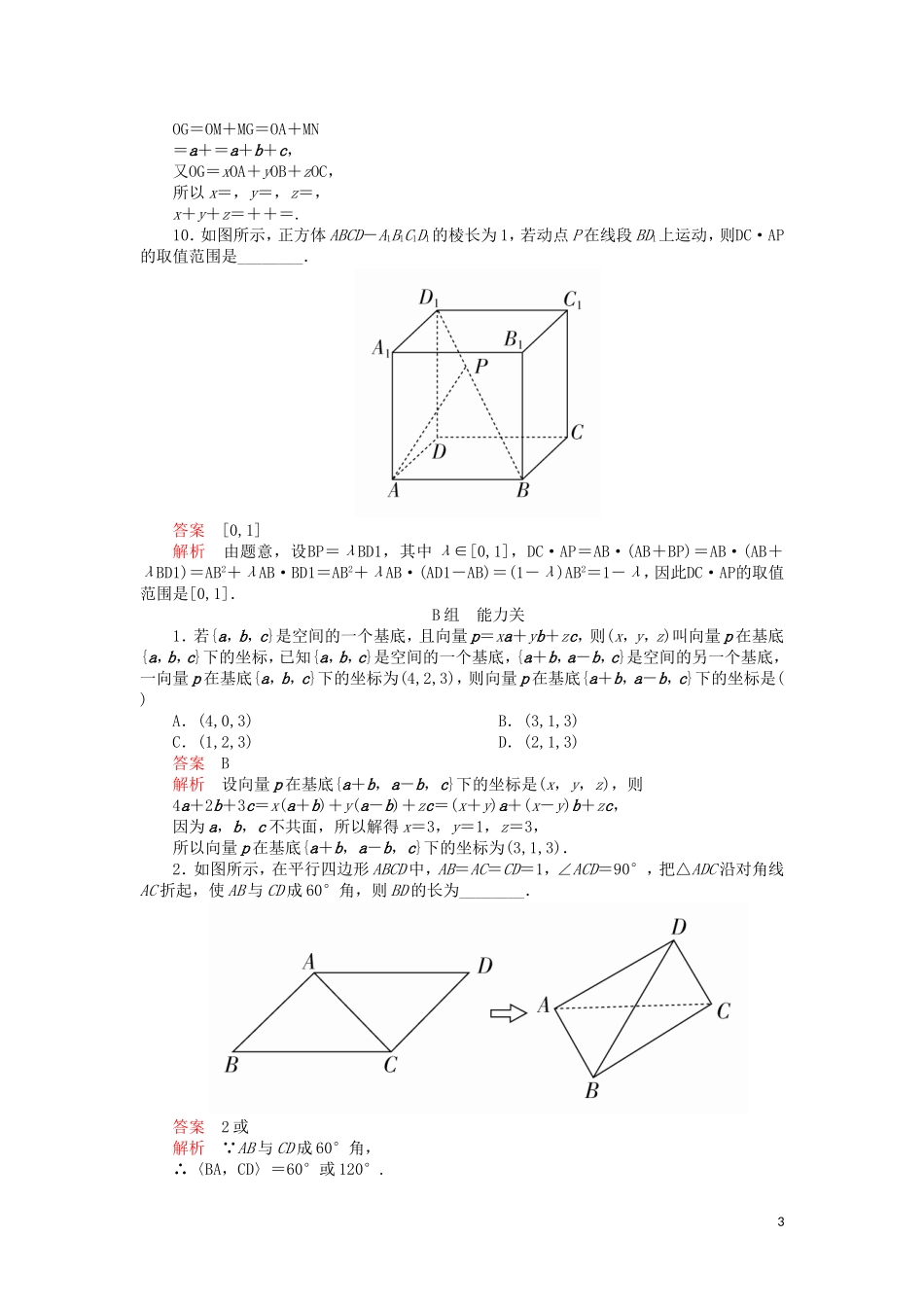
第7章立体几何第6讲A组基础关1.已知点O,A,B,C为空间不共面的四点,且向量a=OA+OB+OC,向量b=OA+OB-OC,则与a,b不能构成空间基底的向量是()A.OAB.OBC.OCD.OA或OB答案C解析根据题意得OC=(a-b),所以OC,a,b共面.故选C.2.(2018·黑龙江齐齐哈尔实验中学期中)设ABCD-A1B1C1D1是棱长为a的正方体,则有()A.AB·C1A=a2B.AB·A1C1=a2C.BC·A1D=a2D.AB·C1A1=a2答案C解析建系如图.则AB·C1A=(a,0,0)·(-a,-a,-a)=-a2,AB·A1C1=(a,0,0)·(a,a,0)=a2,BC·A1D=(0,a,0)·(0,a,-a)=a2,AB·C1A1=(a,0,0)·(-a,-a,0)=-a2,故只有C正确.3.已知a=(1,0,1),b=(x,1,2),且a·b=3,则向量a与b的夹角为()A.B.C.D.答案D解析因为a·b=(1,0,1)·(x,1,2)=x+2=3,所以x=1,所以|a|=,|b|=,所以cos〈a,b〉===.又0≤〈a,b〉≤π,所以〈a,b〉=.4.对于空间一点O和不共线的三点A,B,C,有6OP=OA+2OB+3OC,则()A.O,A,B,C四点共面B.P,A,B,C四点共面C.O,P,B,C四点共面D.O,P,A,B,C五点共面答案B解析解法一:因为6OP=OA+2OB+3OC,所以OP=OA+OB+OC,且++=1,所以A,B,C,P四点共面.解法二:因为6OP=OA+2OB+3OC,所以0=(OA-OP)+2(OB-OP)+3(OC-OP),所以PA+2PB+3PC=0,1所以PC=-PA-PB,所以PC,PA,PB共面,又三个向量有公共点P.所以P,A,B,C四点共面.5.在正方体ABCD-A1B1C1D1中,给出以下向量表达式:①(A1D1-A1A)-AB;②(BC+BB1)-D1C1;③(AD-AB)-2DD1;④(B1D1+A1A)+DD1.其中能够化简为向量BD1的是()A.①②B.②③C.③④D.①④答案A解析①(A1D1-A1A)-AB=AD1-AB=BD1;②(BC+BB1)-D1C1=BC1-D1C1=BD1;③(AD-AB)-2DD1=BD-2DD1≠BD1;④(B1D1+A1A)+DD1=B1D+DD1=B1D1≠BD1.综上,①②符合题意.故选A.6.(2018·舟山模拟)平行六面体ABCD-A1B1C1D1中,向量AB,AD,AA1两两的夹角均为60°,且|AB|=1,|AD|=2,|AA1|=3,则|AC1|等于()A.5B.6C.4D.8答案A解析设AB=a,AD=b,AA1=c,则AC1=a+b+c,|AC1|2=a2+b2+c2+2a·b+2b·c+2c·a=25,因此|AC1|=5.故选A.7.在空间直角坐标系中,已知△ABC的顶点坐标分别为A(1,-1,2),B(5,-6,2),C(1,3,-1),则边AC上的高BD=()A.5B.C.4D.2答案A解析设AD=λAC,AC=(0,4,-3),则AD=(0,4λ,-3λ),AB=(4,-5,0),BD=(-4,4λ+5,-3λ).由AC·BD=0,得λ=-,所以BD=,所以|BD|=5.故选A.8.已知a=(2,3,1),b=(-4,2,x),且a⊥b,则|b|=________.答案2解析因为a⊥b,所以a·b=(2,3,1)·(-4,2,x)=-8+6+x=0,所以x=2.所以|b|==2.9.(2018·郑州模拟)如图所示,已知空间四边形OABC,其对角线为OB,AC,M,N分别为OA,BC的中点,点G在线段MN上,且MG=2GN,若OG=xOA+yOB+zOC,则x+y+z=________.答案解析设OA=a,OB=b,OC=c.则MN=ON-OM=(OB+OC)-OA=b+c-a,2OG=OM+MG=OA+MN=a+=a+b+c,又OG=xOA+yOB+zOC,所以x=,y=,z=,x+y+z=++=.10.如图所示,正方体ABCD-A1B1C1D1的棱长为1,若动点P在线段BD1上运动,则DC·AP的取值范围是________.答案[0,1]解析由题意,设BP=λBD1,其中λ∈[0,1],DC·AP=AB·(AB+BP)=AB·(AB+λBD1)=AB2+λAB·BD1=AB2+λAB·(AD1-AB)=(1-λ)AB2=1-λ,因此DC·AP的取值范围是[0,1].B组能力关1.若{a,b,c}是空间的一个基底,且向量p=xa+yb+zc,则(x,y,z)叫向量p在基底{a,b,c}下的坐标,已知{a,b,c}是空间的一个基底,{a+b,a-b,c}是空间的另一个基底,一向量p在基底{a,b,c}下的坐标为(4,2,3),则向量p在基底{a+b,a-b,c}下的坐标是()A.(4,0,3)B.(3,1,3)C.(1,2,3)D.(2,1,3)答案B解析设向量p在基底{a+b,a-b,c}下的坐标是(x,y,z),则4a+2b+3c=x(a+b)+y(a-b)+zc=(x+y)a+(x-y)b+zc,因为a,b,c不共面,所以解得x=3,y=1,z=3,所以向量p在基底{a+b,a-b,c}下的坐标为(3,1,3).2.如图所示,在平行四边形ABCD中,AB=AC=CD=1,∠ACD=90...