高考数学 考前15天专题突破系列——填空题解题方法突破VIP免费

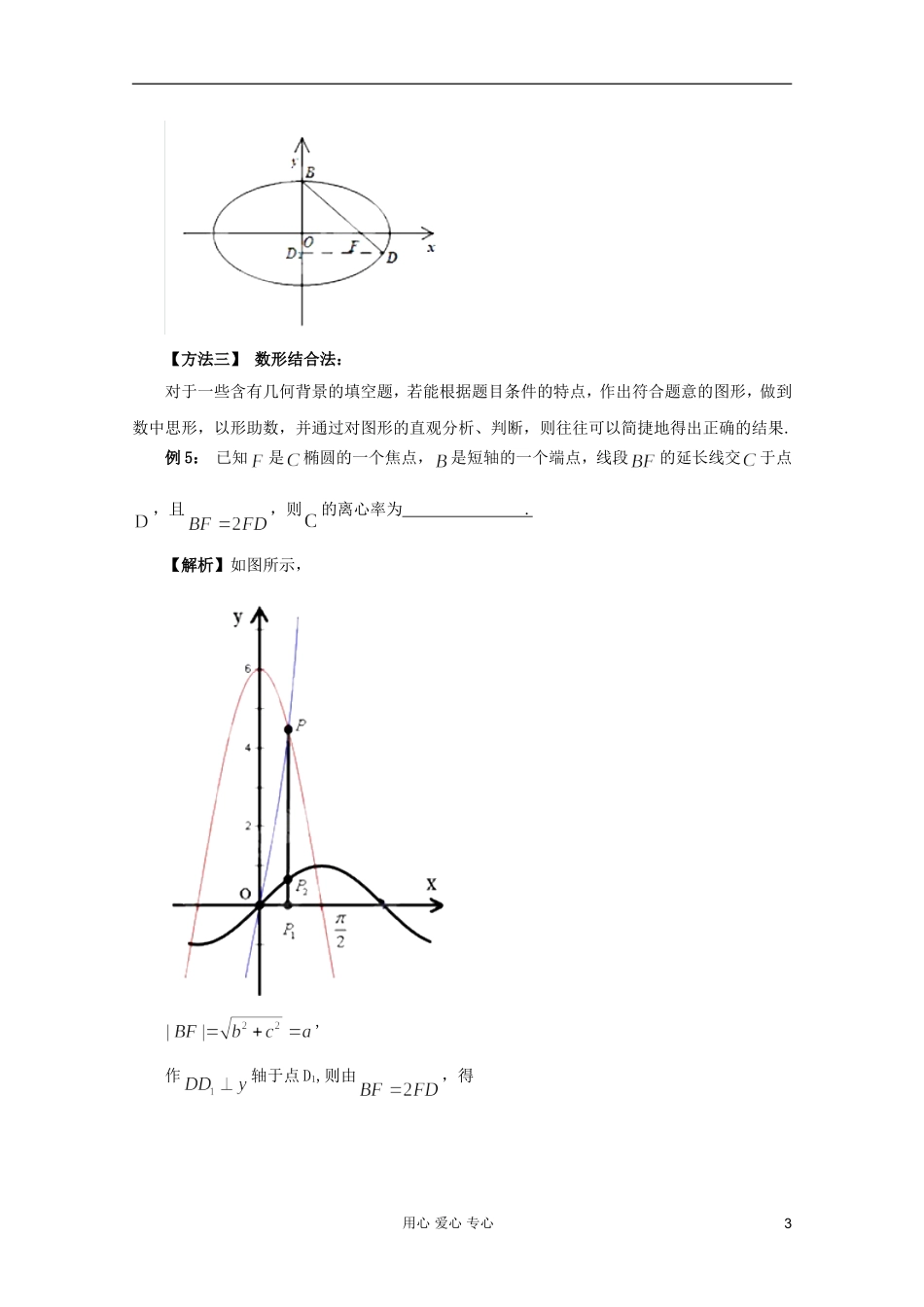
2012年高考数学考前15天专题突破系列——填空题解题方法突破【方法一】直接求解法：直接从题设条件出发，利用定义、性质、定理、公示等，经过变形、推理、计算、判断得到结论.这种方法是解填空题的最基本、最常用的方法.使用直接法解填空题，要善于通过现象看本质，自觉地，有意识地采取灵活、简捷的解法.例1已知双曲线的离心率为2，焦点与椭圆的焦点相同，那么双曲线的焦点坐标为；渐近线方程为.【解析】双曲线焦点即为椭圆焦点，不难算出焦点坐标为，又双曲线离心率为2，即，故，渐近线为.例2某城市缺水问题比较突出，为了制定节水管理办法，对全市居民某年的月均用水量进行了抽样调查，其中4位居民的月均用水量分别为（单位：吨）。根据图2所示的程序框图，若分别为1，1.5，1.5，2，则输出的结果s为.【解析】第一（1i）步：11011ixss第二（2i）步：5.25.1111ixss第三（3i）步：45.15.211ixss第四（4i）步：62411ixss，23641s第五（5i）步：45i，输出23s【方法二】特殊化法：当填空题已知条件中含有某些不确定的量，但填空题的结论唯一或题设条件中提供的信用心爱心专心1息暗示答案是一个定值时，可以将题中变化的不定量选取符合条件的恰当特殊值（特殊函数，特殊角，特殊数列，特殊位置，特殊点，特殊方程，特殊模型等）进行处理，从而得出探求的结论.这样可以大大地简化推理、论证的过程.此种方法也称为“完美法”，其根本特点是取一个比较“完美”的特例，把一般问题特殊化，已达到快速解答.为保证答案的正确性，在利用此方法时，一般应多取几个特例.例3已知定义在上的奇函数满足，且在区间[0，2]上是增函数，若方程（）在区间上有四个不同的根，，则．例4在△中，角所对的边分别为，如果成等差数列，则___________.【解析】取特殊值，则，.或取，则，代入也可得.也可利用正弦定理边化角及三角函数和差化积直接求解。用心爱心专心2【方法三】数形结合法：对于一些含有几何背景的填空题，若能根据题目条件的特点，作出符合题意的图形，做到数中思形，以形助数，并通过对图形的直观分析、判断，则往往可以简捷地得出正确的结果.例5：已知是椭圆的一个焦点，是短轴的一个端点，线段的延长线交于点，且，则的离心率为.【解析】如图所示，,作轴于点D1,则由，得用心爱心专心3,所以,即,由椭圆的第二定义又由,得,整理得.两边都除以,得.例6定义在区间上的函数的图像与的图像的交点为，过点作⊥轴于点，直线与的图像交于点,则线段的长为_____.【解析】线段的长即为的值，且其中的满足，解得，即线段的长为.【特别提醒】考虑通过求出点，的纵坐标来求线段长度，没有想到线段长度的意义，忽略数形结合，导致思路受阻.【方法法四】特征分析法：例7已知函数满足：，，则____________．用心爱心专心4【特别提醒】忽略自变量是一个数值较大的正整数，没有考虑函数值的周期性规律或数列与函数的联系，一味考虑直接求而导致思路受阻.例8五位同学围成一圈依序循环报数，规定：①第一位同学首次报出的数为1.第二位同学首次报出的数也为1，之后每位同学所报出的数都是前两位同学所报出的数之和；②若报出的是为3的倍数，则报该数的同学需拍手一次，当第30个数被报出时，五位同学拍手的总次数为【方法五】构造法：根据题设条件与结论的特殊性，构造出一些熟悉的数学模型，并借助于它认识和解决问题的一种方法.例9如图，在三棱锥中，三条棱，，两两垂直，且>>,分别经过三条棱，，作一个截面平分三棱锥的体积，截面面积依次为，，，则，，的大小关系为.用心爱心专心5【解析】此题考查立体图形的空间感和数学知识的运用能力，已知条件少，没有具体的线段长度，应根据三条棱两两垂直的特点，以，，为棱，补成一个长方体.通过补形，借助长方体验证结论，特殊化，令边长，，分别为1，2，3得..例10已知实数满足，则=____________.【解析】此题考查数学知识的运用能力，两个未知数一个方程，且方程次数较高，不能直接求出，的值，应考虑将整体求出，注意方程的结构特点。构造函数，则已知变为，即，根据函数是奇函数且单调递增可得，于是，即...