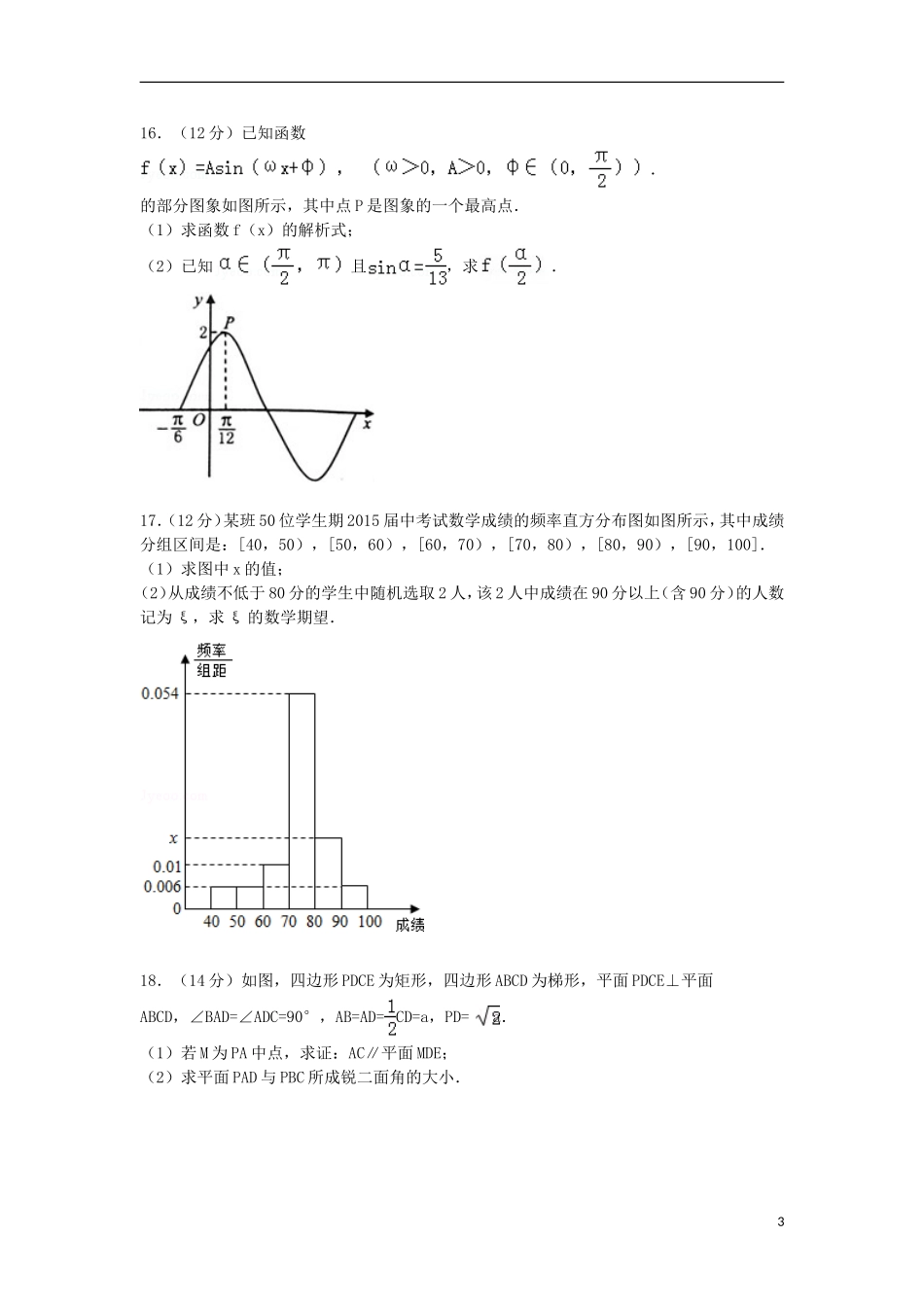
广东省湛江市吴川二中2015届高三上学期11月月考数学试卷(理科)一、选择题:本大题共8小题,每小题5分,共40分.1.(5分)设集合A={x|x+2=0},集合B={x|x2﹣4=0},则A∩B=()A.{﹣2}B.{2}C.{﹣2,2}D.∅2.(5分)复数z=i•(1+i)(i为虚数单位)在复平面上对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.(5分)双曲线2x2﹣y2=8的实轴长是()A.2B.C.4D.4.(5分)已知向量=(1,0),=(,),则下列结论中正确的是()A.||=||B.•=C.与共线D.(﹣)与垂直5.(5分)“x(x﹣3)<0”是“|x﹣1|<2”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.(5分)已知平面α、β和直线m,给出条件:①m∥α;②m⊥α;③m⊂α;④α⊥β;⑤α∥β.由这五个条件中的两个同时成立能推导出m∥β的是()A.①④B.①⑤C.②⑤D.③⑤7.(5分)采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随机编号为1,2,…,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中,编号落入区间[1,450]的人做问卷A,编号落入区间[451,750]的人做问卷B,其余的人做问卷C.则抽到的人中,做问卷B的人数为()A.7B.9C.10D.158.(5分)设A是整数集的一个非空子集,对于k∈A,如果k﹣1∉A,且k+1∉A,那么称k是A的一个“好元素”.给定S={1,2,3,4,5,6,7,8},由S的3个元素构成的所有集合中,不含“好元素”的集合共有()A.6个B.12个C.9个D.5个二、填空题(本大题共5小题,分为必做题和选做题两部分.每小题5分,满分25分)(一)必做题:第9至13题为必做题,每道试题考生都必须作答.9.(5分)已知f(x)=lnx+的定义域为.10.(5分)若曲线y=kx+lnx在点(1,k)处的切线平行于x轴,则k=.111.(5分)若等差数列{an}和等比数列{bn}满足a1=b1=1,a2=b2=2.则a5b5=.12.(5分)按如图的程序框图运行后,输出的S应为.13.(5分)已知△ABC的内角A,B,C的对边分别为a,b,c,且c=,B=120°,则△ABC的面积等于.(二)选做题:第14、15题为选做题,考生只选做其中一题.【极坐标与参数方程】14.(3分)在极坐标系中,直线ℓ1的方程是ρsin(θ+)=,以极点为原点,以极轴为x轴的正半轴建立直角坐标系,在直角坐标系中,直线ℓ2的方程是3x+ky=1.如果直线ℓ1与ℓ2垂直,则常数k=.【几何证明选讲】15.(3分)如图,在△ABC中,DE∥BC,EF∥CD,若BC=3,DE=2,DF=1,则BD的长为、AB的长为.三、解答题:本大题共6小题,满分79分,解答应写出文字说明,证明过程或演算步骤.216.(12分)已知函数.的部分图象如图所示,其中点P是图象的一个最高点.(1)求函数f(x)的解析式;(2)已知且,求.17.(12分)某班50位学生期2015届中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].(1)求图中x的值;(2)从成绩不低于80分的学生中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为ξ,求ξ的数学期望.18.(14分)如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=CD=a,PD=a.(1)若M为PA中点,求证:AC∥平面MDE;(2)求平面PAD与PBC所成锐二面角的大小.319.(14分)已知数列{an}的前n项和是Sn,且Sn+an=1(n∈N*).(1)求数列{an}的通项公式;(2)设bn=log3(1﹣Sn+1)(n∈N*),求适合方程的正整数n的值.20.(13分)如图,已知椭圆C:,其左右焦点为F1(﹣1,0)及F2(1,0),过点F1的直线交椭圆C于A,B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D,E两点,且|AF1|、|F1F2|、|AF2|构成等差数列.(1)求椭圆C的方程;(2)记△GF1D的面积为S1,△OED(O为原点)的面积为S2.试问:是否存在直线AB,使得S1=S2?说明理由.21.(14分)设函数f(x)=(x﹣1)ex﹣kx2(k∈R).(1)当k=1时,求函数f(x)的单调区间;(2)当时,求函数f(x)在[0,k]上的最大值M.广东省湛江市吴川二中2015届高三上学期11月月考数学试卷(...