函数yAsinwxf的图象第课时平行班教学设计VIP免费

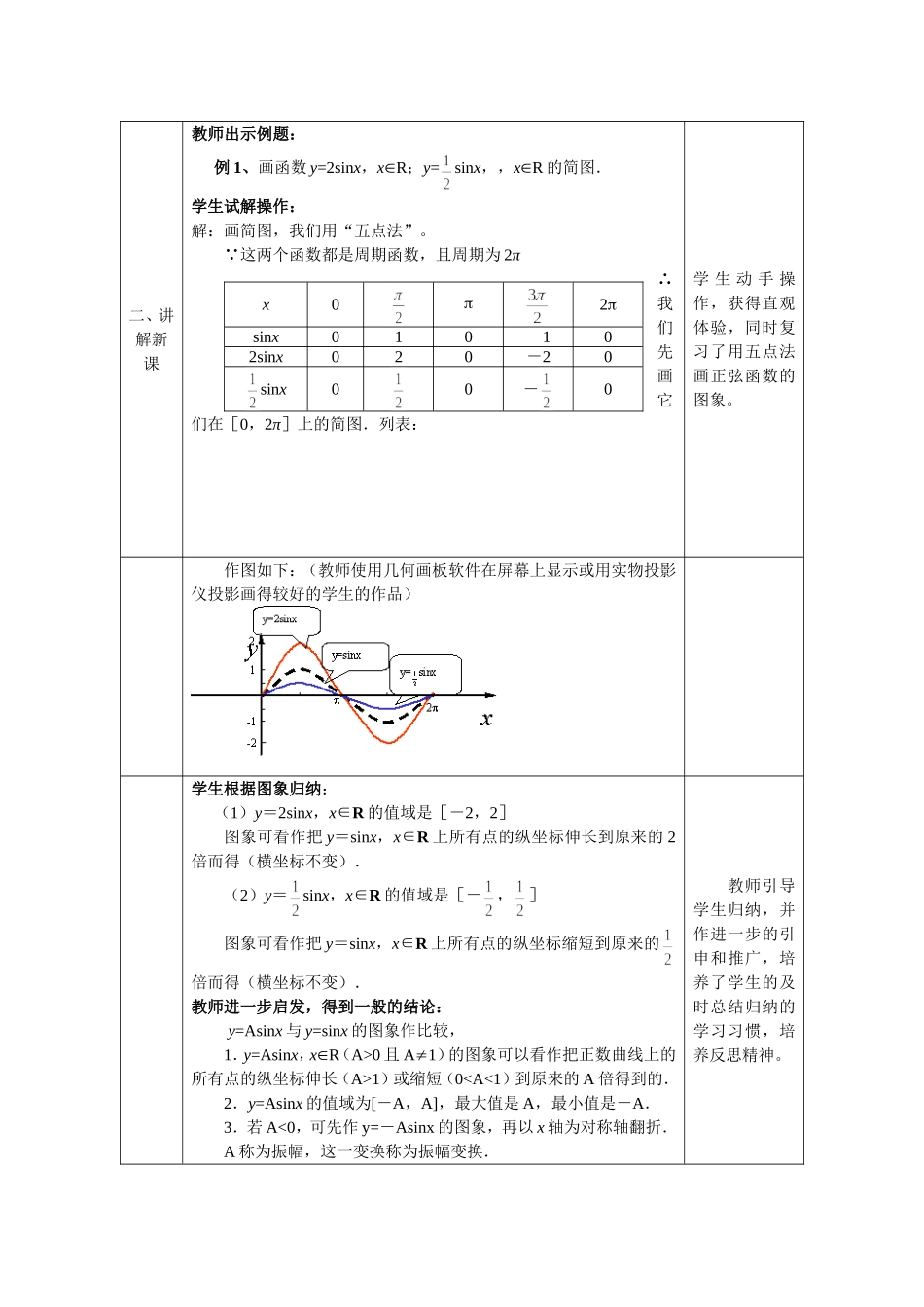
1.5函数y=Asin（wx+f）的图象【课题】：函数y=Asin（wx+f）的图象（1）方案二：【设计与执教者】：广州六中江玉军gzjyj@163.com部分资料引用自新疆奎屯市一中王新敞的教学设计。【教学时间】：1课时【学情分析】：本课是在学生已经学习了诱导公式、正弦函数和余弦函数的图象之后的一节新授课，学生对于正弦、余弦函数的图象已经有了基本的了解。另外，虽然在必修1函数的教学中，学生也已经接触过函数图象的变换（左加右减，上加下减）知识，部分学生经过一段时间之后已经有一些遗忘。【教学目标】：（1）理解振幅、频率、相位等概念的物理意义；（2）会用五点法画出函数y=Asin（x+）的简图，明确参数A、、对函数图象的影响作用，能说出函数y=Asin（x+）的图象是由y=Asinx的图象如何变换而得到的。【教学重点】：讨论函数y=Asin（x+）的图象变换过程。【教学难点】：函数y=Asin（x+）的两种不同的图象变换过程的区别与联系。【教学突破点】：通过几何画板课件的演示，突破教学难点。【教法、学法设计】：多媒体辅助教学，变式教学；观察归纳法，小组讨论法。【课前准备】：几何画板课件。【教学过程设计】：教学环节教学活动设计意图一、课程引入教师讲解：在现实生活中，我们常常会遇到形如y＝Asin（ωx＋）的函数解析式（其中A，ω，都是常数）．下面我们讨论函数y＝Asin（ωx＋），x∈R的简图的画法，从函数图象中得出各个参数A、ω和对函数图象的影响．开门见山，点出本节课要研究的主要问题，同时让学生带着问题学习，使学生的观察有一定的目的性。二、讲解新课教师出示例题：例1、画函数y=2sinx，xR；y=sinx，，xR的简图．学生试解操作：解：画简图，我们用“五点法”。 这两个函数都是周期函数，且周期为2π∴我们先画它们在［0，2π］上的简图．列表：学生动手操作，获得直观体验，同时复习了用五点法画正弦函数的图象。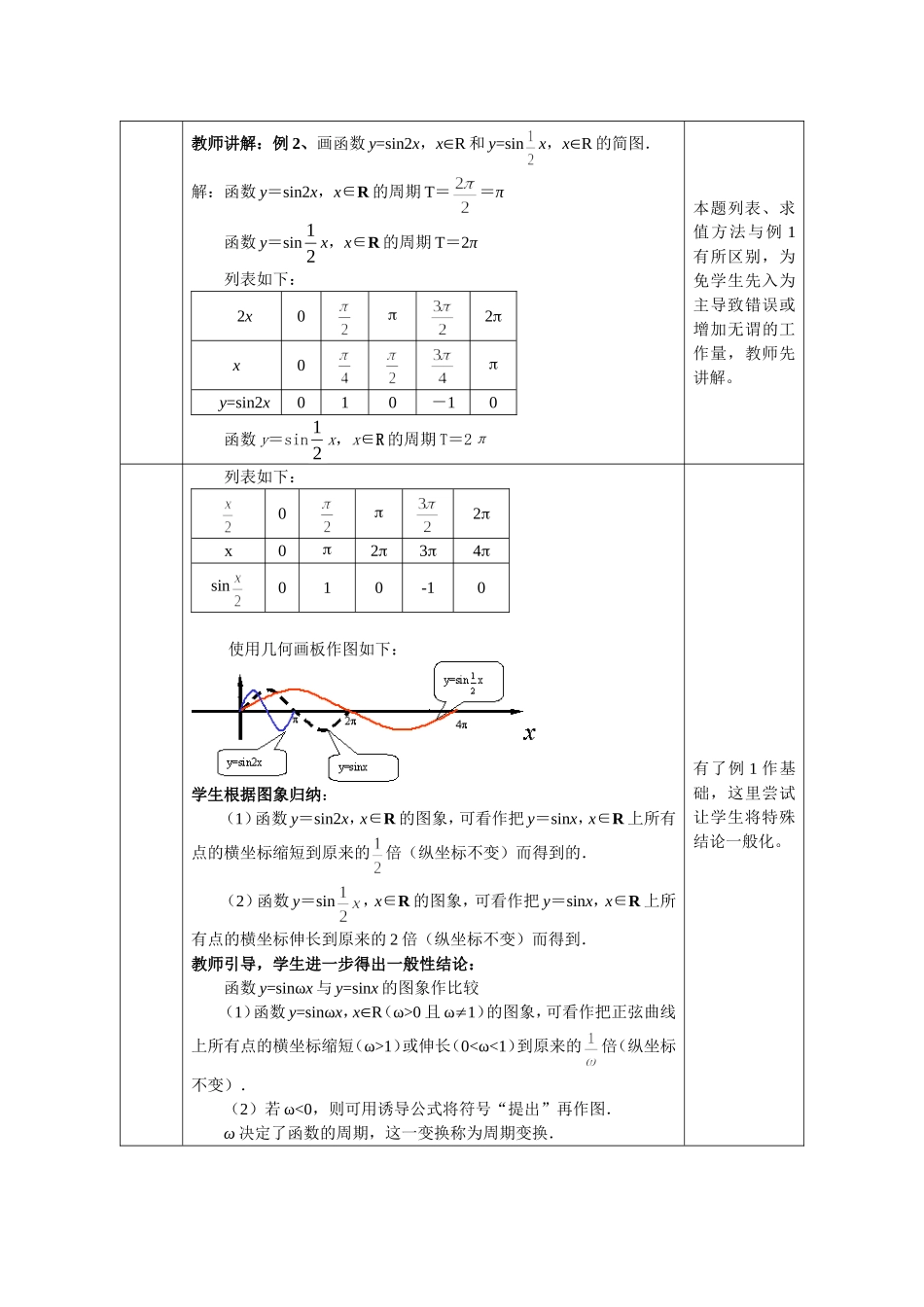作图如下：（教师使用几何画板软件在屏幕上显示或用实物投影仪投影画得较好的学生的作品）学生根据图象归纳：（1）y＝2sinx，x∈R的值域是［－2，2］图象可看作把y＝sinx，x∈R上所有点的纵坐标伸长到原来的2倍而得（横坐标不变）．（2）y＝sinx，x∈R的值域是［－，］图象可看作把y＝sinx，x∈R上所有点的纵坐标缩短到原来的倍而得（横坐标不变）．教师进一步启发，得到一般的结论：y=Asinx与y=sinx的图象作比较，1．y=Asinx，xR（A>0且A1）的图象可以看作把正数曲线上的所有点的纵坐标伸长（A>1）或缩短（00且ω1）的图象，可看作把正弦曲线上所有点的横坐标缩短（ω>1）或伸长（0<ω<1）到原来的倍（纵坐标不变）．（2）若ω<0，则可用诱导公式将符号“提出”再作图．ω决定了函数的周期，这一变换称为周期变换．有了例1作基础，这里尝试让学生将特殊结论一般化。教师出示例题例3．画出函数y＝sin（x＋），x∈R和y＝sin（x－），x∈R的简图．学生解答：解：列表x－x+02sin（x+）010–10xX－02sin（x–）010–10...