广东省湛江二中港城中学高中数学 第一章 立体几何高考题型 新人教A版必修2VIP免费

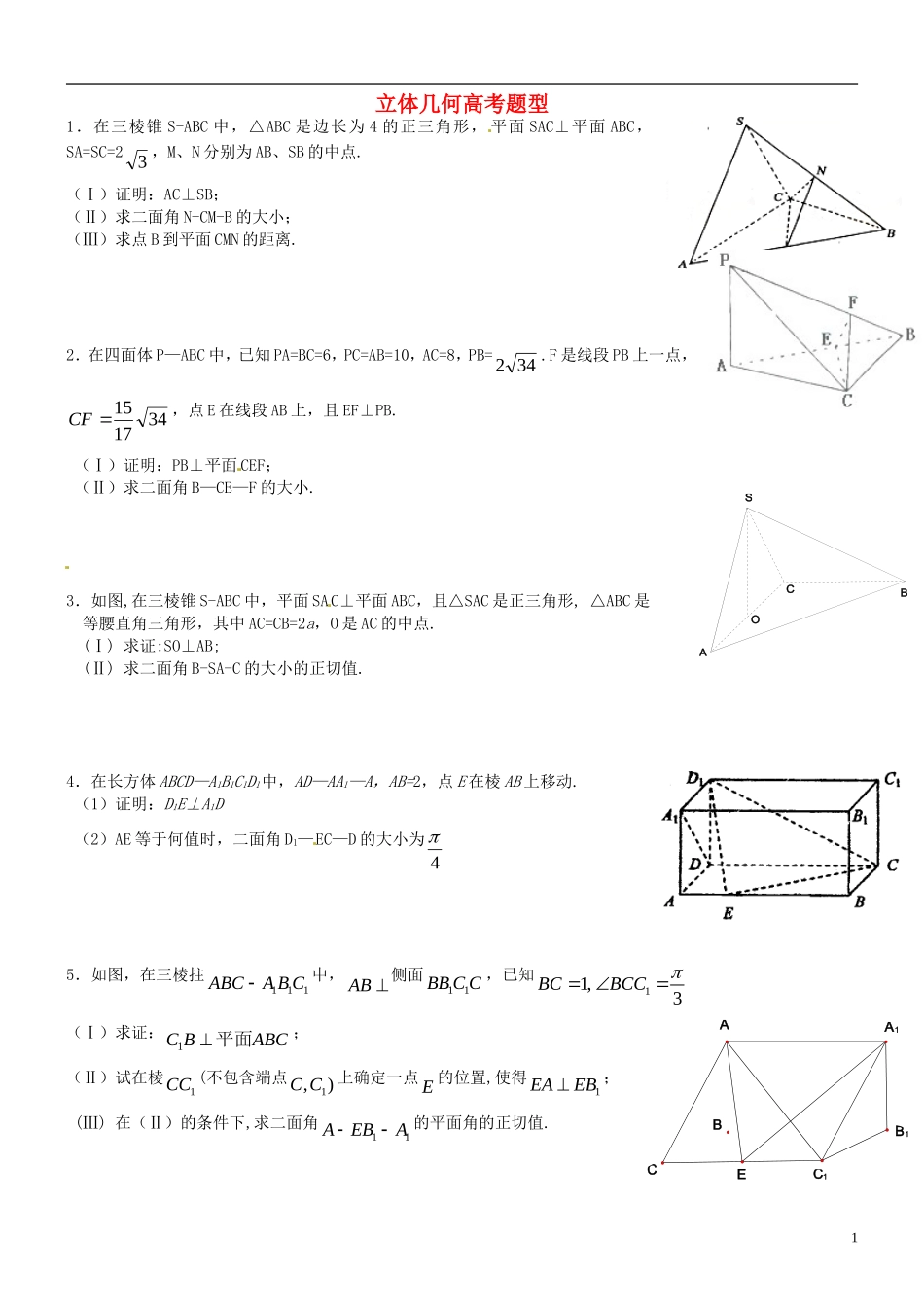
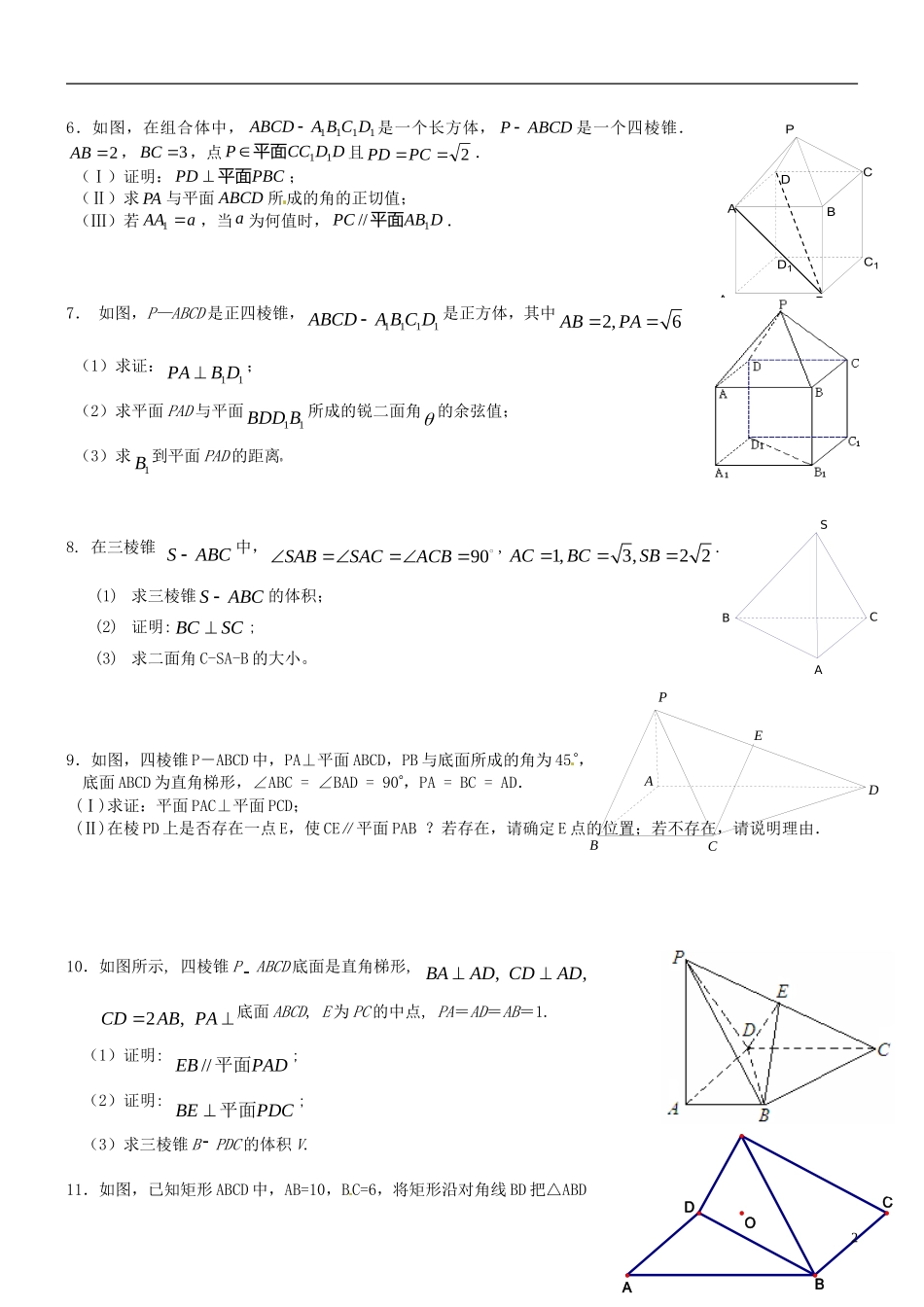
CBAOSEC1B1A1CBA立体几何高考题型1．在三棱锥S-ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=23，M、N分别为AB、SB的中点.（Ⅰ）证明：AC⊥SB；（Ⅱ）求二面角N-CM-B的大小；（Ⅲ）求点B到平面CMN的距离.2．在四面体P—ABC中，已知PA=BC=6，PC=AB=10，AC=8，PB=342.F是线段PB上一点，341715CF，点E在线段AB上，且EF⊥PB.（Ⅰ）证明：PB⊥平面CEF；（Ⅱ）求二面角B—CE—F的大小.3．如图,在三棱锥S-ABC中，平面SAC⊥平面ABC，且△SAC是正三角形,△ABC是等腰直角三角形，其中AC=CB=2a，O是AC的中点.(Ⅰ)求证:SO⊥AB;(Ⅱ)求二面角B-SA-C的大小的正切值.4．在长方体ABCD—A1B1C1D1中，AD—AA1—A，AB=2，点E在棱AB上移动.（1）证明：D1E⊥A1D（2）AE等于何值时，二面角D1—EC—D的大小为45．如图，在三棱拄111ABCABC中，AB侧面11BBCC，已知11,3BCBCC（Ⅰ）求证：1CBABC平面；（Ⅱ）试在棱1CC(不包含端点1,)CC上确定一点E的位置,使得1EAEB；(Ⅲ)在（Ⅱ）的条件下,求二面角11AEBA的平面角的正切值.1GCGBGAGSOA1DCBA6．如图，在组合体中，1111DCBAABCD是一个长方体，ABCDP是一个四棱锥．2AB，3BC，点DDCCP11平面且2PCPD．（Ⅰ）证明：PBCPD平面；（Ⅱ）求PA与平面ABCD所成的角的正切值；（Ⅲ）若aAA1，当a为何值时，DABPC1//平面．7．如图，P—ABCD是正四棱锥，1111ABCDABCD是正方体，其中2,6ABPA（1）求证：11PABD；（2）求平面PAD与平面11BDDB所成的锐二面角的余弦值；（3）求1B到平面PAD的距离新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆8.在三棱锥SABC中，90SABSACACB,1,3,22ACBCSB.(1)求三棱锥SABC的体积；(2)证明:BCSC;(3)求二面角C-SA-B的大小。9．如图，四棱锥P－ABCD中，PA⊥平面ABCD，PB与底面所成的角为45，底面ABCD为直角梯形，∠ABC=∠BAD=90，PA=BC=AD．(Ⅰ)求证：平面PAC⊥平面PCD；(Ⅱ)在棱PD上是否存在一点E，使CE∥平面PAB？若存在，请确定E点的位置；若不存在，请说明理由．10．如图所示,四棱锥PABCD底面是直角梯形,,,BAADCDAD2,CDABPA底面ABCD,E为PC的中点,PA＝AD＝AB＝1.（1）证明://EBPAD平面;（2）证明:BEPDC平面;（3）求三棱锥BPDC的体积V.11．如图，已知矩形ABCD中，AB=10，BC=6，将矩形沿对角线BD把△ABD2D1C1B1A1PDCBAADEPCBFEDCBAP折起，使A移到1A点，且1A在平面BCD上的射影O恰好在CD上．（Ⅰ）求证：1BCAD；（Ⅱ）求证：平面1ABC平面1ABD；（Ⅲ）求三棱锥1ABCD的体积．12．如图3所示，四棱锥PABCD中，底面ABCD为正方形，PD平面ABCD，2PDAB，E，F，G分别为PC、PD、BC的中点．（1）求证：PAEF；（2）求二面角D－FG－E的余弦值．13．如图，直四棱柱ABCD—A1B1C1D1的高为3，底面是边长为4且∠DAB=60°的菱形，AC∩BD=O，A1C1∩B1D1=O1，E是O1A的中点.（1）求二面角O1－BC－D的大小；（2）求点E到平面O1BC的距离.14如图,在四棱锥PABCD中,底面ABCD是边长为a的正方形,侧面PAD底面ABCD，且22PAPDAD,若E、F分别为PC、BD的中点.(Ⅰ)EF//平面PAD；(Ⅱ)求证:平面PDC平面PAD；(Ⅲ)求二面角BPDC的正切值.15如图，已知长方体ABCD—A1B1C1D1，AB=2，AA1=1，直线BD与平面AA1B1B所成的角为30°，AE⊥BD于E，F为A1B1的中点.（1）求异面直线AE与BF所成的角；（2）求平面BDF与平面AA1B1B所成的二面角（锐角）的大小；（3）求点A到平面BDF的距离.3图3ABCDEFGPEO1OD1C1B1DCBAA1EDCBAP16如图，四棱锥P—ABCD中，PB⊥底面ABCD，CD⊥PD，底面ABCD为直角梯形，AD∥BC，AB⊥BC，AB=AD=PB=3，点E在棱PA上，且PE=2EA。（1）求异面直线PA与CD所成的角；（2）求证：PC//平面EBD；（3）求二面角A—BE—D的余弦值。17．如图，已知四棱锥PABCD的底面ABCD是菱形；PA平面ABCD,PAADAC，点F为PC的中点．（Ⅰ）求证：//PA平面BFD；（Ⅱ）求二面角CBFD的正切值．18如图，PA⊥平面ABCD，四边形ABCD是矩形，E、F分别是AB、PD的中点.（1...