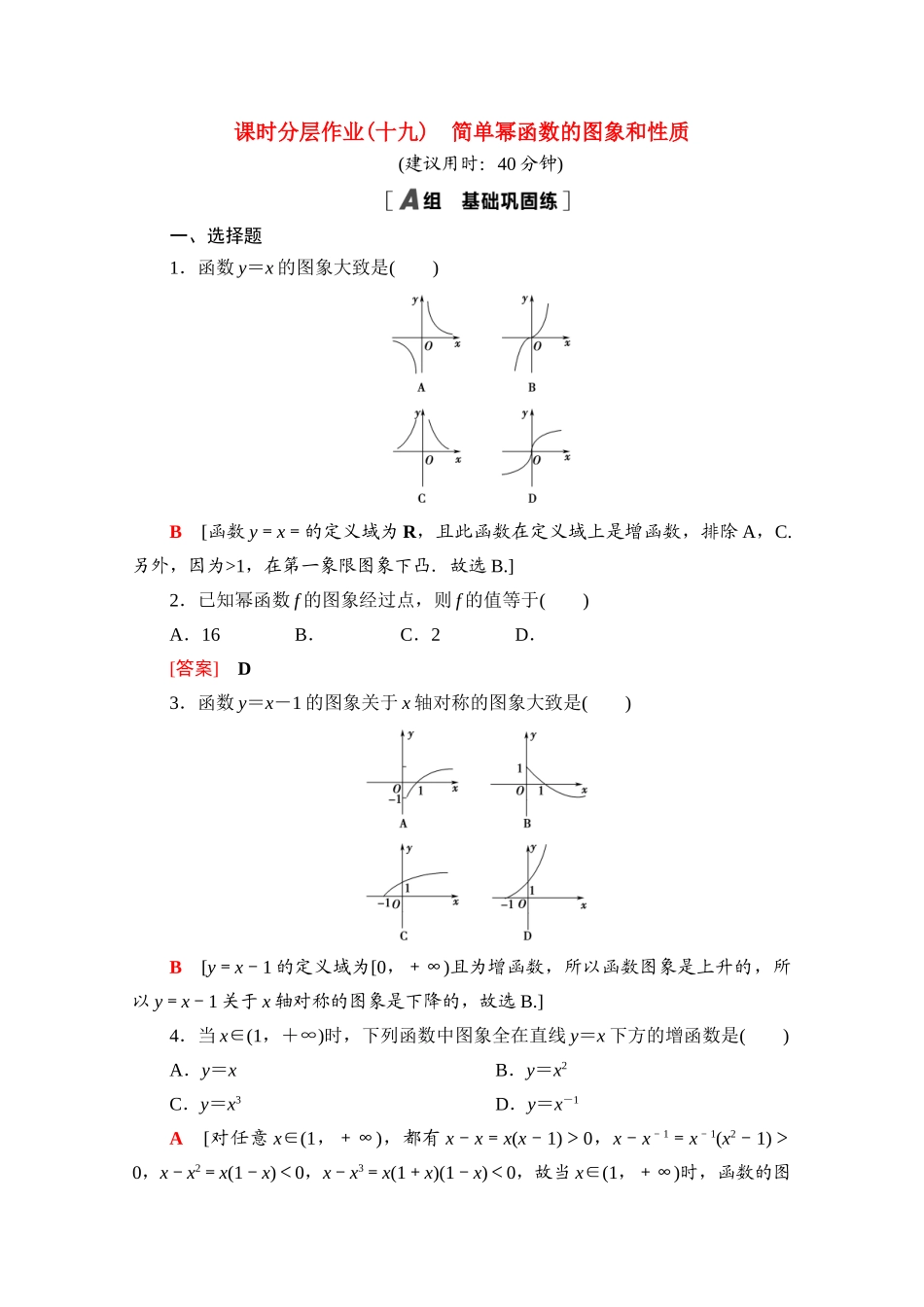
课时分层作业(十九)简单幂函数的图象和性质(建议用时:40分钟)一、选择题1.函数y=x的图象大致是()B[函数y=x=的定义域为R,且此函数在定义域上是增函数,排除A,C.另外,因为>1,在第一象限图象下凸.故选B.]2.已知幂函数f的图象经过点,则f的值等于()A.16B.C.2D.[答案]D3.函数y=x-1的图象关于x轴对称的图象大致是()B[y=x-1的定义域为[0,+∞)且为增函数,所以函数图象是上升的,所以y=x-1关于x轴对称的图象是下降的,故选B.]4.当x∈(1,+∞)时,下列函数中图象全在直线y=x下方的增函数是()A.y=xB.y=x2C.y=x3D.y=x-1A[对任意x∈(1,+∞),都有x-x=x(x-1)>0,x-x-1=x-1(x2-1)>0,x-x2=x(1-x)<0,x-x3=x(1+x)(1-x)<0,故当x∈(1,+∞)时,函数的图象全在直线y=x下方的函数有y=x和y=x-1,而函数y=x是单调递增函数,函数y=x-1是单调递减函数,所以选A.]5.已知幂函数f=(n2+2n-2)xn2-3n(n∈Z)在(0,+∞)上是减函数,则n的值为()A.-3B.1C.2D.1或-3B[由于f为幂函数,所以n2+2n-2=1,解得n=1或n=-3,当n=-3时,f(x)=x18在(0,+∞)是增加的,不合题意,故选B.]二、填空题6.判断大小:5.25-1________5.26-1.(填“>”或“<”)>[ y=x-1在(0,+∞)上是减函数,又5.25<5.26,∴5.25-1>5.26-1.]7.函数f=(x+3)-2的单调增区间是________.(-∞,-3)[y=x-2=的增区间为(-∞,0),y=(x+3)-2是由y=x-2向左平移3个单位长度得到的.∴y=(x+3)-2的单调增区间为(-∞,-3).]8.已知幂函数f=xm2-1(m∈Z)的图象与x轴,y轴都无交点,且关于原点对称,则函数f的解析式是________.f=x-1[ 函数的图象与x轴,y轴都无交点,∴m2-1<0,解得-1
-2.5,∴(-2)-3<(-2.5)-3.(2) 幂函数y=x在(0,+∞)上为增函数,又8=,>,∴>,∴8>.10.已知函数f=(m∈R),试比较f(5)与f(-π)的大小.[解]f===m-=m-(x-1)-2.f的图象可由y=x-2的图象首先作关于x轴的对称变换,然后向右平移1个单位长度,再向上(m≥0)(或向下(m<0))平移|m|个单位长度得到(如图所示).显然,图象关于x=1对称且在(1,+∞)上单调递增,∴f(-π)=f(2+π),而2+π>5,∴f(-π)=f(2+π)>f(5).11.如图是幂函数y=xm和y=xn在第一象限内的图象,则()A.-11D.n<-1,m>1B[由题图知,y=xm在[0,+∞)上是增函数,y=xn在(0,+∞)上为减函数,所以m>0,n<0.又当x>1时,y=xm的图象在y=x的下方,y=xn的图象在y=x-1的下方,所以m<1,n<-1,从而0B.f(|AB|+|CD|),∴f>,故选A.]13.已知幂函数f(x)=xα,当x>1时,恒有f(x)0D.α<0B[ x>1,∴xα