3.2一元二次不等式及其解法(一)VIP免费

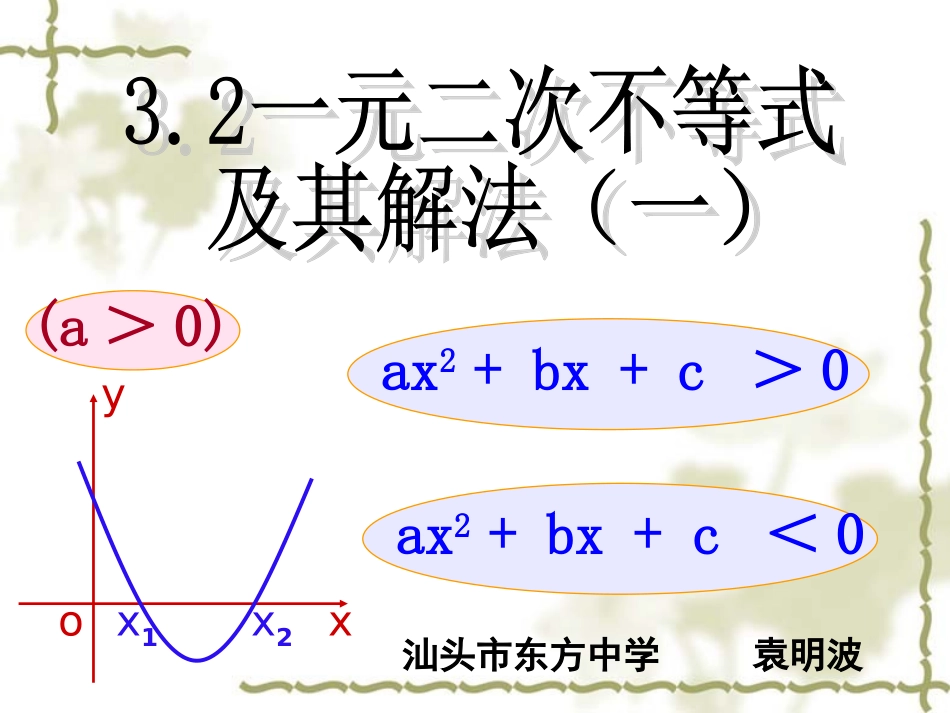
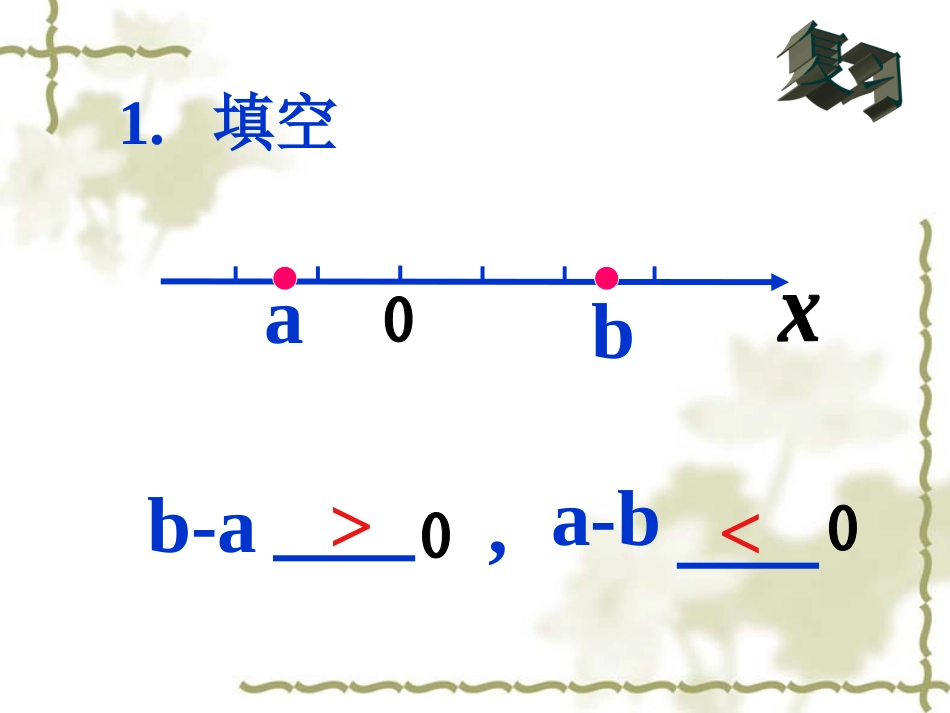
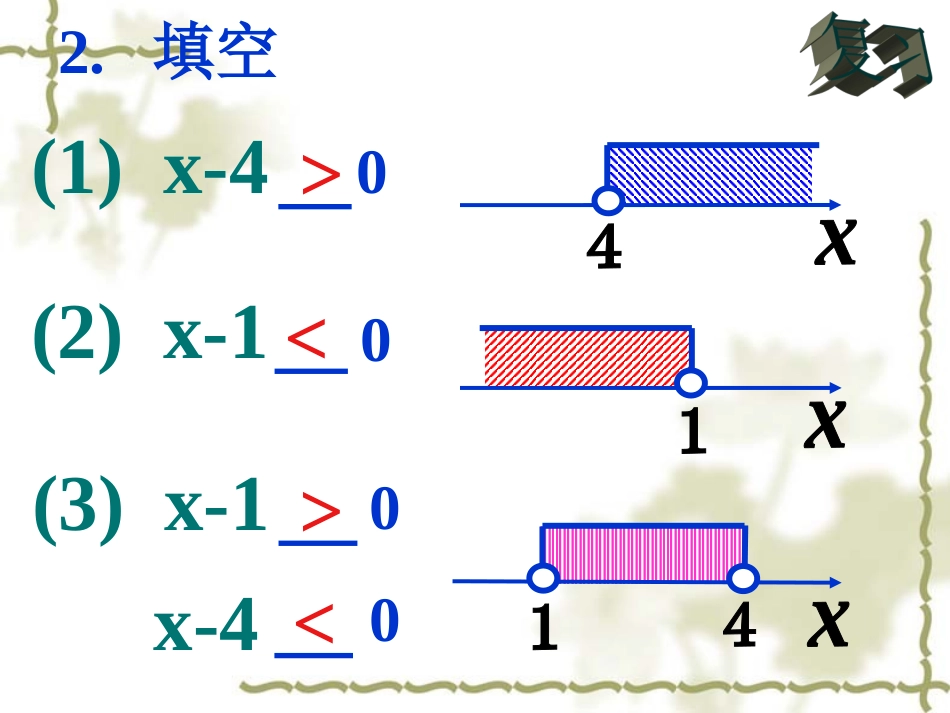
xyx1x2oax2+bx+c＞0ax2+bx+c＜0(a＞0)汕头市东方中学袁明波<>ab1.填空a-bb-a,<>2.填空(1)x-40(3)x-100x-4><(2)x-103.解方程：x2-x-6=0解：x1=-2,x2=3(x+2)(x-3)=0将方程左边的二次三项式x2-x-6因式分解,得两个网络服务公司（InternetSericeProvider）的资费标准：电信：每小时收费1.5元网通：用户上网的第一小时内收费1.7元，第二小时内收费1.6元，以后每小时减少0.1元.（若用户一次上网时间超过17小时，按17小时计算）<不妨设该同学一次上网不超过17小时>一次上网在多长时间以内能够保证选择电信比选择网通所需费用少？新课导入分析：假设一次上网x小时，1.7，1.6，1.5，1.4，……是以1.7为首项，以-0.1为公差的等差数列 ∴网通公司的收取费用为)1.0(2)1(7.1xxx20)35(xx如果能够保证选择电信公司比选择网通公司所需费用少，则20)35(5.1xxx整理得052xx新课导入则电信公司的收取费用为1.5x根据题意知，网通收费1.7，1.6，1.5，1.4，……这是什么？一、定义：一般地，只含有一个未知数，且未知数的最高次数为2的不等式，叫做一元二次不等式。注意：（1）只含有一个未知数x；（2）未知数的最高次数为2.新知讲解二、一般表达式一元二次不等式的一般表达式是22220(000axbxcaxbxcaxbxcaxbxc或或或）(a0)，其中a、b、c为常数.练习：判断下列式子是不是一元二次不等式？56a)1(2xx03)2(xy0)3)(2()3(xx)1(3)4(2xxxx探究新知思考：那么一元二次不等式怎样去求解呢？052xx22250550.xxyxxx已知一元二次不等式，一元二次函数，一元二次方程x问题1：二次函数与x轴交点坐标是多少？答：（0，0）、（5，0）.问题2：一元二次方程根是什么？答：x1=0，x2=5.问题3：问题1中的坐标与问题2中的根有何内在联系？答：交点的横坐标为方程的根.05y25yxx问题4：满足什么条件，函数图象在x轴上方？答：x>5或x<0问题5：能否利用问题4得出不等式x2-5x>0的解集呢？问题7：能否利用问题6得出不等式x2-5x<0的解集呢？答：能，不等式的解集为50xxx或05y25yxx问题6：满足什么条件，函数图象在x轴下方？答：05x答：能，不等式的解集为05xx一元二次不等式的解法判别式△=b2-4acy=ax2+bx+c(a>0)的图象ax2+bx+c=0(a>0)的根ax2+bx+c>0(a>0)的解集ax2+bx+c<0(a>0)的解集x1x2xyOyxOx1yxO△>0△=0△<0有两相异实根x1,x2(x1x2}{x|x10且△>0）解一元二次不等式的步骤：（1）化为标准形式（注意把二次项系数化为正数）；（4）联系二次函数的图象得出不等式的解集（注意结果要写成集合或者区间的形式）.特别地，若一元二次不等式的左边的二次三项式能分解因式，则可立即写出不等式的解集（在两根之内或两根之外）.yx1x2x（2）确定判别式的符号；24bac（3）若则求出该不等式对应的二次方程的根；若则对应的二次方程无根；0，0，例题讲解【例1】求不等式的解集.24410xx解:所以原不等式的解集为｛x︱x≠｝12而方程的根是2(21)0x12x原不等式可化为2(21)0x【例2】求不等式的解集2230xx解：不等式可化为2230xx △=-8<0方程无实数根2230xx而的图象开口向上223yxx∴原不等式的解集为22(1)76(2)9610(3)(3)(2)1xxxxxxxxx解下列关于的不等式2(1)76xx解：原不等式可化为2760xx而方程的两个根是X1=1，x2=62760xx∴原不等式的解集为16xx解：而方程的根是2(31)0x13x13xx∴原不等式的解集为22)610x（9x原不等式可化为2(31)0x(3)(3-)(2)1xxxx解：原不等式可化为2210xx而方程的两个根是2210xx121,12xx∴原不等式的解集是112xxx或本课小结本课小结1.一元二次不等式的定义及一般表达式（1）把二次项系数化为正数；（2）解对应的一元二次方程；（3）根据方程的根，结合不等式方向及二次函数图象；（4）得出不等式的解集（...