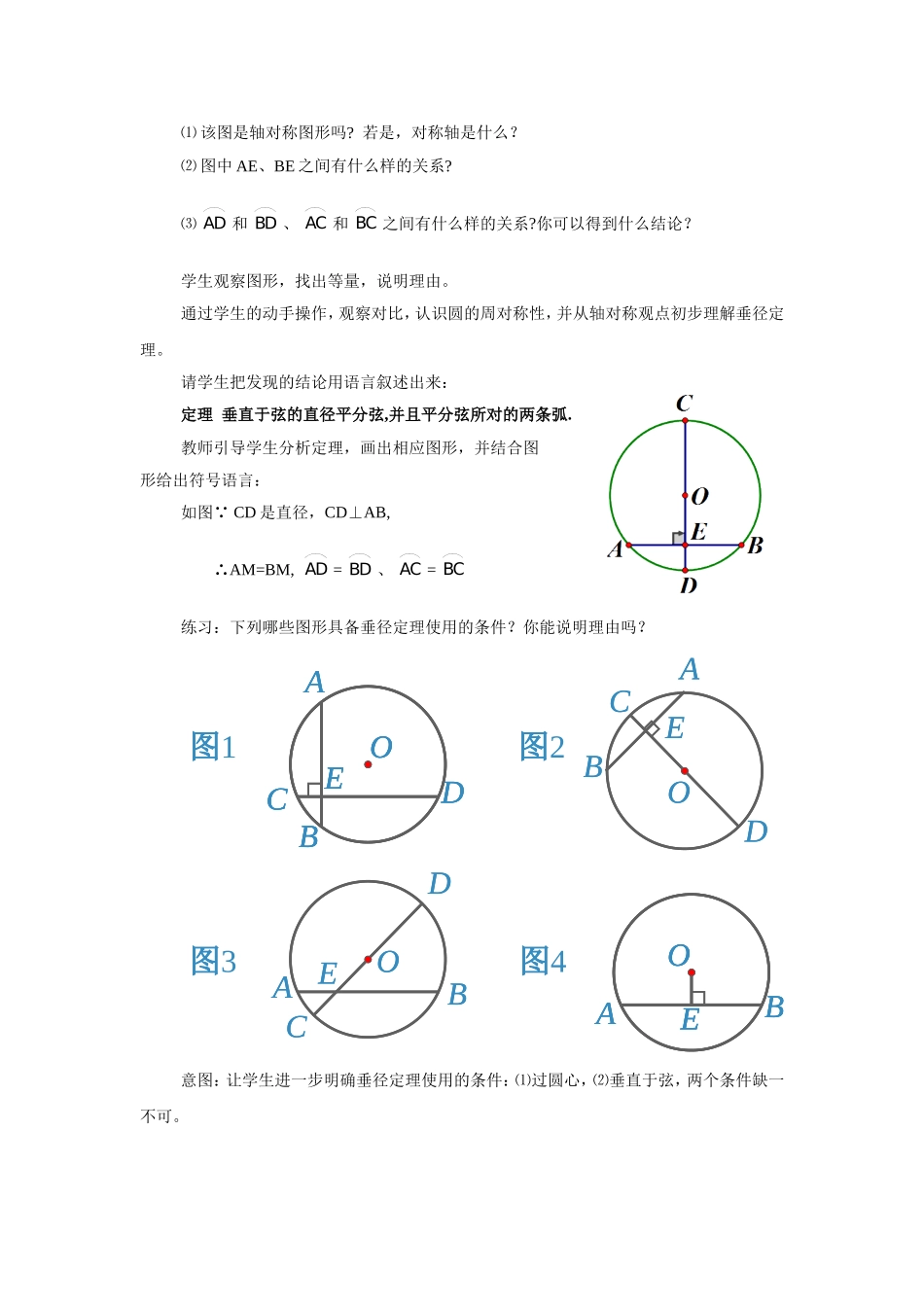
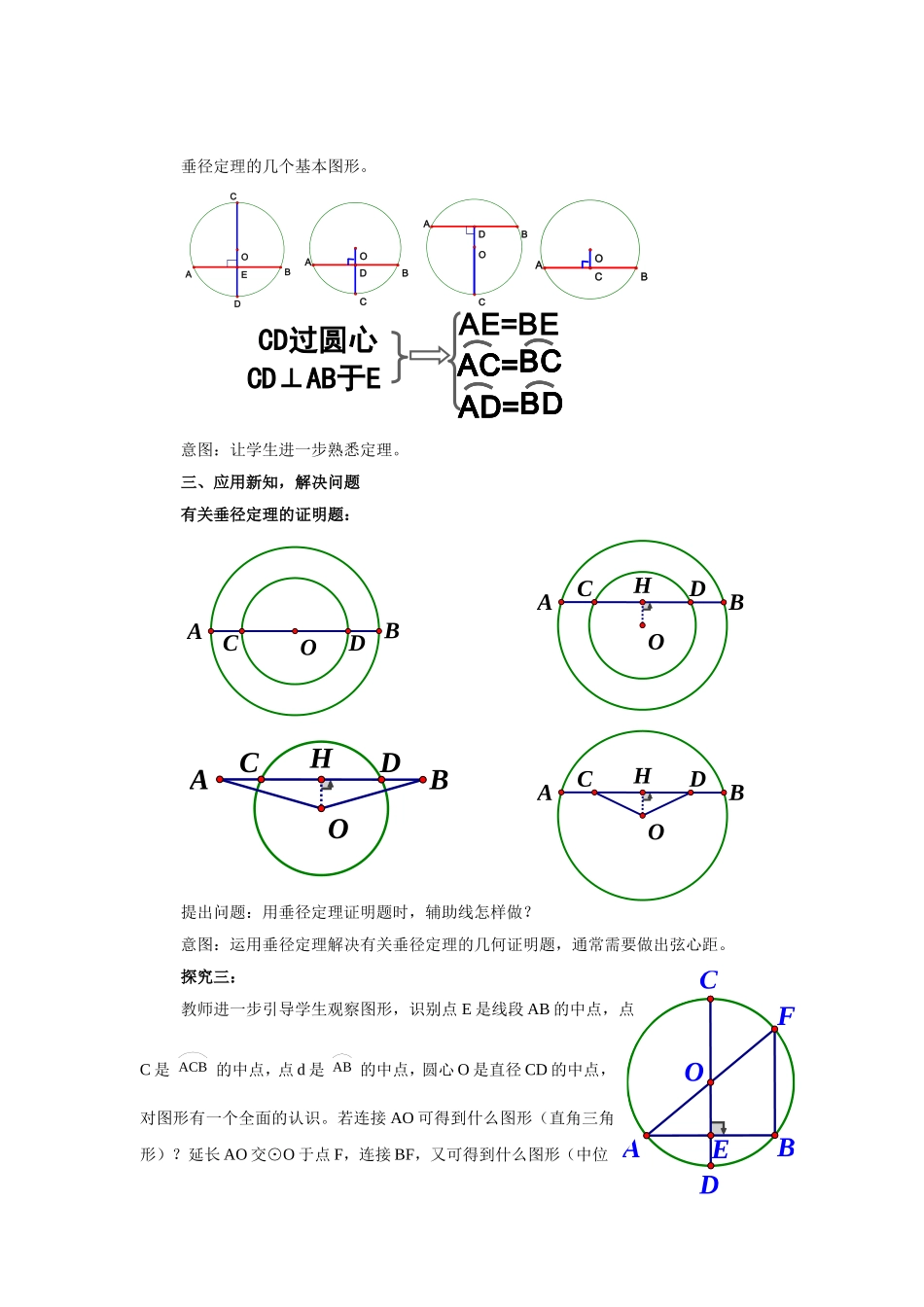
OABDCEDCOAB垂直于弦的直径(2课时)第1课时灵宝市实验中学裴斌鑫教学目标1.理解圆的轴对称性;2.理解垂径定理,会运用垂径定理解决简单的证明、计算问题;3.通过经历对垂径定理的认识过程,培养观察问题、独立思考、深入分析的能力。学情分析学生两级分化严重,学优生所占比例偏小;学生学习主动性不足,缺乏自信,回答问题的声音不大;部分学生分析能力、计算能力、概括能力不足。教学重难点重点:垂径定理及其应用难点:垂径定理的应用教学过程一、课前练习,巩固基础1、线段是轴对称图形吗?若是,它的对称轴是什么?2、什么是等弧?长度相等的弧是等弧吗?3、在右图中,弦AB所对的弧有几条?分别是什么?二、创设情境,探究新知探究一:在一张纸上画一个圆,做出这个圆的一条直径,把圆形纸片沿直线对折,你发现了什么?由此你能得到什么结论?教师提问,学生观察发现:圆是轴对称图形,经过圆心的每一条直线都是它的对称轴,圆的对称轴有无数条。探究二:1、在纸上画一个圆,在圆中作图:任意做一条弦AB,过圆心O做与AB垂直的直径CD交AB于E。2、已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E⑴该图是轴对称图形吗?若是,对称轴是什么?⑵图中AE、BE之间有什么样的关系?⑶AD和BD、AC和BC之间有什么样的关系?你可以得到什么结论?学生观察图形,找出等量,说明理由。通过学生的动手操作,观察对比,认识圆的周对称性,并从轴对称观点初步理解垂径定理。请学生把发现的结论用语言叙述出来:定理垂直于弦的直径平分弦,并且平分弦所对的两条弧.教师引导学生分析定理,画出相应图形,并结合图形给出符号语言:如图 CD是直径,CD⊥AB,∴AM=BM,AD=BD、AC=BC练习:下列哪些图形具备垂径定理使用的条件?你能说明理由吗?DOCAEBDOCAEBDOCAEBDOCAEBDOCAEB图1图2图3图4OAEBOAEBOAEBDOCAEBDOCAEB意图:让学生进一步明确垂径定理使用的条件:⑴过圆心,⑵垂直于弦,两个条件缺一不可。HDCOABDCOABHDCOABHDCOABEFDCOAB垂径定理的几个基本图形。EDCOABOBCADDOBCAOBACCD过圆心CD⊥AB于EAE=BEAC=BCAC=AC=BCBCAD=BDAD=AD=BDBD意图:让学生进一步熟悉定理。三、应用新知,解决问题有关垂径定理的证明题:提出问题:用垂径定理证明题时,辅助线怎样做?意图:运用垂径定理解决有关垂径定理的几何证明题,通常需要做出弦心距。探究三:教师进一步引导学生观察图形,识别点E是线段AB的中点,点C是ACB的中点,点d是AB的中点,圆心O是直径CD的中点,对图形有一个全面的认识。若连接AO可得到什么图形(直角三角形)?延长AO交⊙O于点F,连接BF,又可得到什么图形(中位a/2drhEDCOAB线基本图形)?意图:在教师的引导下,通过对图形的变化发展学生的想象力,培养学生学生构造图形的意识。如图,已知在⊙O中,弦AB的长为a,圆心O到AB的距离OE为d,⊙O的半径OA为r,弓形高DE为h。r=d+h注意:1、在r、d、a、h四个量中,知二求二;2、只有当已知a,h,求d、r时需要设未知数列方程求解.有关垂径定理的计算题:例如图,在⊙O中,弦AB=8cm,圆心O到AB的距离OE=3cm,求⊙O的半径。解:连接OA. OE⊥AB∴AE=AB=4cm,在RT△OAE中,AE=4cm,OE=3cm∴OA==5cm.即⊙O的半径为5cm.方法:见垂径,连半径,构造直角三角形。意图:结合垂径定理的基本图形,借助勾股定理进行计算练习:1、如图,在⊙O中,半径OD=10cm,DE=2cm,直径CD⊥AB于点E,求弦AB的长。2、如图,在⊙O中,弦AB=8cm,DE=2cm,直径CD⊥AB于点E,求圆的半径的长。EFOABPHOABP注意:已知弦长和弓形高,求圆的半径时需要设未知数列方程求解.意图:通过练习体会在圆中,若知道圆的半径、圆心到弦的距离、弦长三个量中的任意两个量。可根据勾股定理求出第三个量。四、课堂小结,形成经验通过这节课的学习你有哪些收获?意图:引导学生总结,教师补充。五、课堂检测,及时反馈1、如图,点A、B是⊙O上两点,AB=8,点P是⊙O上的动点(P与A、B不重合),连接AP、BP,过点O分别作OE⊥AP于E,OF⊥BP于F,则EF=。2、如图,已知AB是⊙O的弦,P是AB上一点AB=10cm,PB=4cm,PO=5cm则⊙O的半径等于cm。意图:及时了解学生学习效果,对于学生在测验中出现的问题有针对性的...