直线和圆的位置关系公开课课件VIP免费

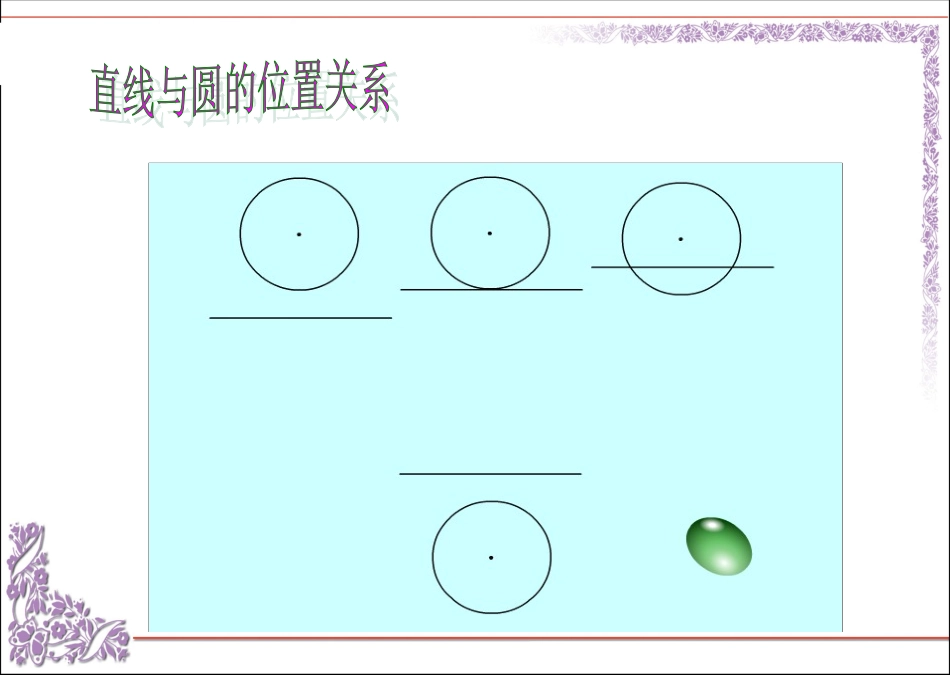
a.O图1b.A.O图2c.F.E.O图3这时直线叫做圆的割线,公共点叫直线与圆的交点。直线与圆没有没有公共点时,叫做直线与圆相离.直线与圆有唯一唯一公共点时,叫做直线与圆相切.直线与圆有两个两个公共点时,叫做直线与圆相交.这时直线叫做圆的切线,唯一公共点叫做直线与圆的切点。1.1.直线与圆的位置关系直线与圆的位置关系((图形特图形特征征))1.能否根据基本概念来判断直线与圆的位置关系？思考直线l与⊙O没有公共点直线l与⊙O相离．直线l与⊙O只有一个公共点直线l与⊙O相切．直线l与⊙O有两个公共点直线l与⊙O相交．2.是否还有其他的方法判断直线与圆的位置关系？ddd.O.O.Orrr相离相切相交1、直线与圆相离=>d>r2、直线与圆相切=>d=r3、直线与圆相交=>dd>r2、直线与圆相切=>d=r3、直线与圆相交=>dr没有lrdOlrdBAOlrdAO例题1：OXY已知⊙A的直径为6，点A的坐标为（-3，-4），则⊙A与X轴的位置关系是_____,A⊙与Y轴的位置关系是______。BC43相离相切.A例题2：圆的直径是13cm，如果直线与圆心的距离分别是①4.5cm；②6.5cm；③8cm，那么直线和圆分别是什么位置关系？有几个公共点？例题3：分析在RtABC△中，∠C=90°，AC=3cm，BC=4cm，以C为圆心，r为半径的圆与AB有怎样的位置关系？为什么？（1）r=2cm；（2）r=2.4cm(3)r=3cm。BCAD4532.4cm2.4cm解：过C作CDAB⊥，垂足为D。在RtABC△中，AB===5（cm）根据三角形面积公式有CD·AB=AC·BC222根据直线与圆的位置关系的数量特征，应该用圆心到直线的距离d与半径r的大小进行比较；关键是确定圆心C到直线AB的距离d，这个距离是什么呢？怎么求这个距离？即圆心C到AB的距离d=2.4cm。（1）当r=2cm时，∵d＞r，∴⊙C与AB相离。（2）当r=2.4cm时，∵d=r，∴⊙C与AB相切。（3）当r=3cm时，∵d＜r，∴⊙C与AB相交。解：过C作CDAB⊥，垂足为D。在RtABC△中，AB===5（cm）根据三角形面积公式有CD·AB=AC·BC∴CD==2222=2.4（cm）。ABCAD453d=2.4d=2.4例:RtABC,C=90°AC=△∠3cm，BC=4cm，以C为圆心，r为半径的圆与AB有怎样的位置关系？为什么？（1）r=2cm；（2）r=2.4cm(3)r=3cm。例题4：）如图，某船向正东方向航行，在A处望见某岛C在北偏东60°方向，前进6海里到B点，测得该岛在北偏东30°方向。已知该岛5.2海里内有暗礁，若该船继续向东航行，有无触礁危险？请说明理由。（参考数据：）732.132.识别直线与圆的位置关系的方法：（1）一种是根据定义进行识别：直线l与⊙O没有公共点直线l与⊙O相离．直线l与⊙O只有一个公共点直线l与⊙O相切．直线l与⊙O有两个公共点直线l与⊙O相交．（2）另一种是根据圆心到直线的距离d与圆半径r的大小关系来进行识别：d>r直线l与⊙O相离；d=r直线l与⊙O相切；d