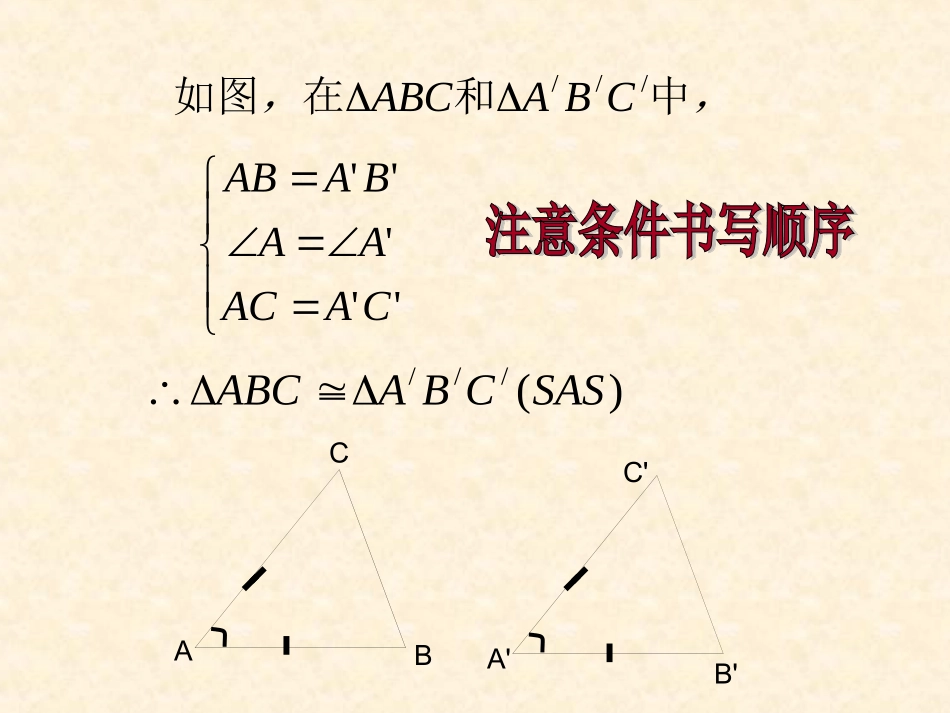
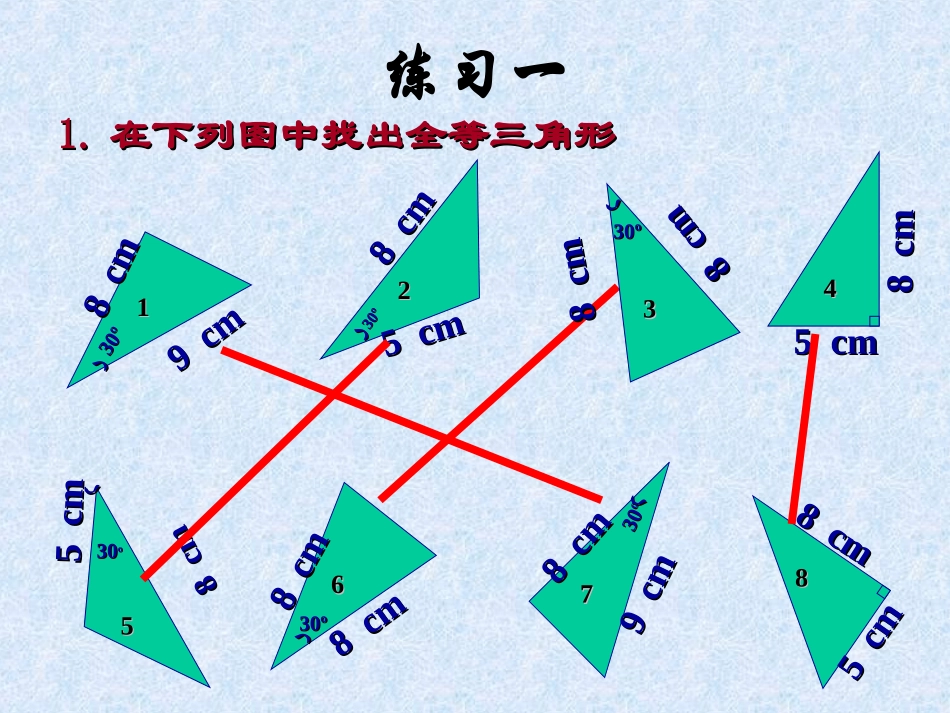
14.214.2全等三角形的判定(全等三角形的判定(11))边角边公理边角边公理有两边和它们的夹角对应相等的两个有两边和它们的夹角对应相等的两个三角形全等三角形全等..(简写(简写““边角边边角边””或或““SASSAS””))'''''CAACAABAAB,CBAABC,中和在如图///)(///SASCBAABCABCA'C'B'1.1.在下列图中找出全等三角形在下列图中找出全等三角形11رر3030ºº8cm8cm9cm9cm66رر3030ºº8cm8cm8cm8cmⅣⅣ448cm8cm5cm5cm223030ººرر8cm8cm5cm5cm553030ºº8cm8cmرر5cm5cm888cm8cm5cm5cmرر3030ºº8cm8cm9cm9cm77ⅢⅢرر3030ºº8cm8cm8cm8cm33练习一CABDO2.2.在下列推理中填写需要补充在下列推理中填写需要补充的条件,使结论成立:的条件,使结论成立:(1)(1)如图,在△如图,在△AOBAOB和△和△DOCDOC中中AO=DO(AO=DO(已知已知))______=________()______=________()BO=CO(BO=CO(已知已知))∴△∴△AOBDOC≌△AOBDOC≌△()()∠∠AOBAOB∠∠DOCDOC对顶角相等对顶角相等SASSAS(2)(2)如图,在△如图,在△AECAEC和△和△ADBADB中,中,AEAE==ADAD((已知已知))_____=______()_____=______()ACAC==ABAB((已知已知))∴△∴△AECADB≌△AECADB≌△()()AEBDCSAS∠∠AA∠∠AA公共角AECBDA3.已知:如图,AC=AD,∠CAB=∠DAB.求证:BC=BD.BACD证明:在△证明:在△ACBACB和△和△ADBADB中,中,AC=AD(AC=AD(已知已知))∠∠CAB=∠DAB(CAB=∠DAB(已知已知))AB=AB(AB=AB(公共边公共边))∴△∴△ACB≌△ADBACB≌△ADB((SASASS))∴∴BC=BD(BC=BD(全等三角形的对应边相等全等三角形的对应边相等))如图,有一池塘,要测池塘两端如图,有一池塘,要测池塘两端AA、、BB的距离,的距离,可在平地上取一个可直接到达可在平地上取一个可直接到达AA和和BB的点的点CC,,连结连结ACAC并延长至并延长至DD使使CD=CACD=CA,连结,连结BCBC并延长并延长至至EE使使CE=CBCE=CB,连结,连结EDED,那么量出,那么量出DEDE的长,的长,就是就是AA、、BB的距离,为什么?的距离,为什么?解决问题解决问题BBAADDEECC证明:在△证明:在△ABCABC和△和△DECDEC中,中,AC=DC(AC=DC(已知已知))∠∠ACB=∠DCE(ACB=∠DCE(对顶角相等对顶角相等))BC=EC(BC=EC(已知已知))∴△∴△ABC≌△DECABC≌△DEC((SASSAS))∴∴AB=DEAB=DE((全等三角形的对应边相等全等三角形的对应边相等))探究:以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40°,情况又怎样?动手画一画,你发现了什么?ABCDEF2.5cm3.5cm40°40°3.5cm2.5cm结论:两边及其一边所对的角相等,两个三角形不一定全等拓展由由““两边及其中一边的对角对应相等两边及其中一边的对角对应相等(SSA)(SSA)””能否判定两个三角形全等?能否判定两个三角形全等?AABCDBCD如图,在△如图,在△ABCABC和△和△ABDABD中,中,AB=AB(AB=AB(公共边公共边))AC=AD(AC=AD(已知已知))∠∠BB=∠B(=∠B(公共公共角角))但△但△ABCABC和△和△ABDABD不全等不全等..练习二1.已知:如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.ABCDFE5.已知:如图,AC⊥BD,C为垂足,AC=DC,CB=CE.求证:DF⊥AB.ABEFCD课堂小结1.边角边公理:有两边和它们的______对应相等的两个三角形全等(SAS)夹角2.边角边公理的发现过程所用到的数学方法(包括画图、实验、猜想、分析、归纳等.)3.边角边公理的应用中所用到的数学方法:证明线段(或角相等)证明线段(或角)所在的两个三角形全等.转化1.公理中所出现的边与角必须在所证明的两个三角形中.2.公理中涉及的角必须是两边的夹角.3.要充分利用图形中的隐含条件,如公共边、公共角、对顶角等用公理证明两个三角形全等需注意