一圆周角定理VIP免费

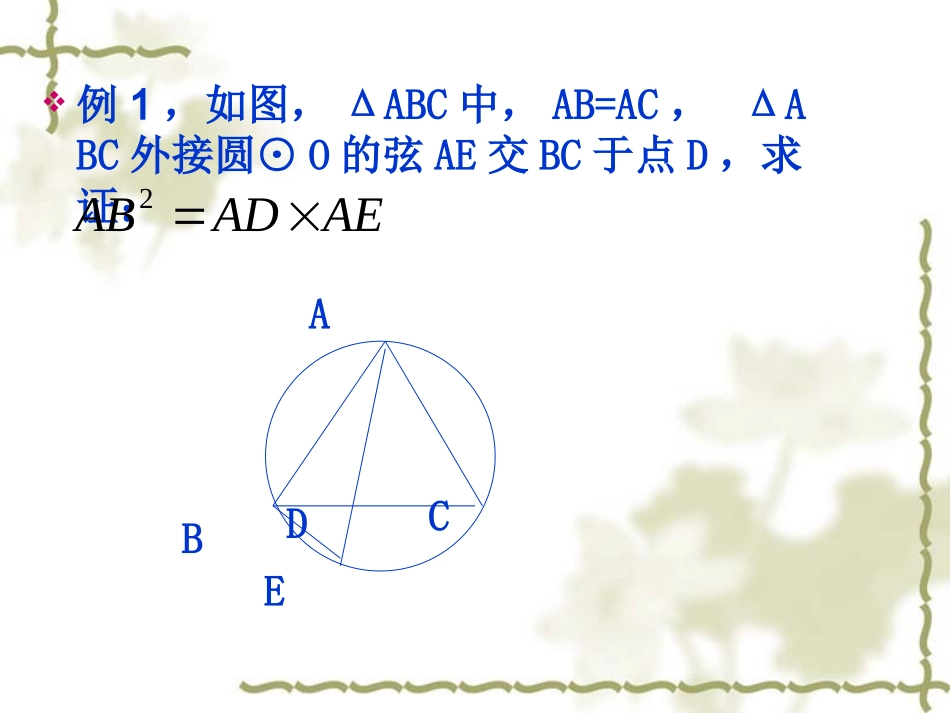
圆周角定理圆周角的定义：顶点在圆周上且两边都与圆相交的角。圆周角定理：圆周角的度数等于其所对弧的度数的一半。推论1：同弧（或等弧）上的圆周角相等。同圆或等圆中，相等的圆周角所对的弧相等。推论2：半圆（或直径）上的圆周角等于90度。反之，90度的圆周角所对的弦为直径。例1，如图，ΔABC中，AB=AC，ΔABC外接圆⊙O的弦AE交BC于点D，求证：AEADAB2BAECD例2，如图，设AD,CF是ΔABC的两条高,AD,CF的延长线交ΔABC的外接圆O于G,AE是⊙O的直径,求证:(1)AB·AC=AD·AE(2)DG=DH·OAHFEDCBG例３，如图，BC是半圆的直径,P是半圆上的一点,过的中点Ａ，作ＡＤ⊥ＢＣ，垂足为Ｄ，ＢＰ交ＡＤ于Ｅ，交ＡＣ于Ｆ，求证：ＢＥ＝ＡＥ＝ＥＦBPＡＢＥＤＣＰＦ︵1234例４，如图，ΔABC内接于⊙Ｏ，ＡＨ⊥ＢＣ于点Ｈ，求证：（１）∠ＯＡＢ＝∠ＨＡＣ（２）ＯＡ·ＡＨ＝１／２ＡＢ·ＡＣ．ＡＯＨＣＢD