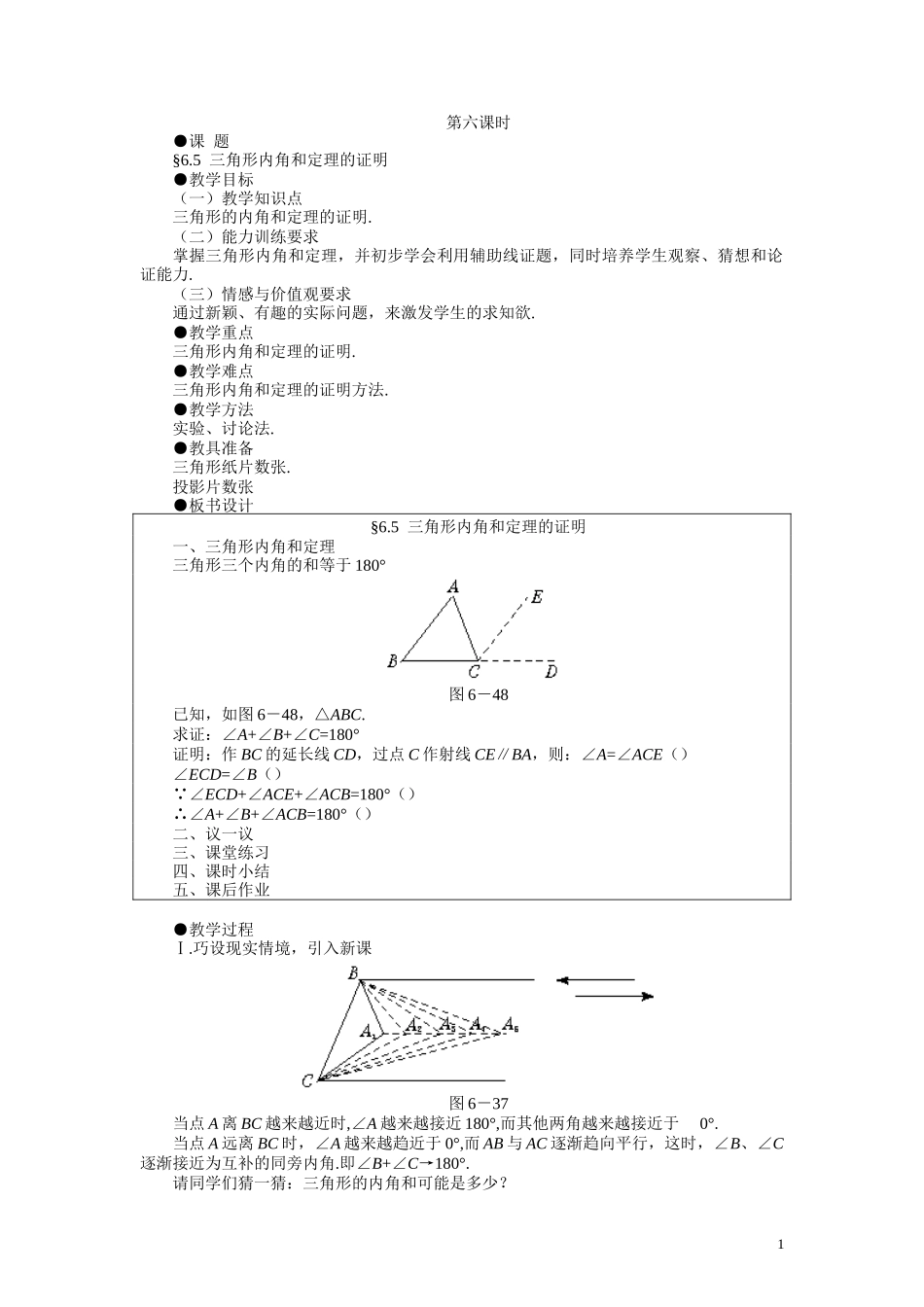
第六课时●课题§6.5三角形内角和定理的证明●教学目标(一)教学知识点三角形的内角和定理的证明.(二)能力训练要求掌握三角形内角和定理,并初步学会利用辅助线证题,同时培养学生观察、猜想和论证能力.(三)情感与价值观要求通过新颖、有趣的实际问题,来激发学生的求知欲.●教学重点三角形内角和定理的证明.●教学难点三角形内角和定理的证明方法.●教学方法实验、讨论法.●教具准备三角形纸片数张.投影片数张●板书设计§6.5三角形内角和定理的证明一、三角形内角和定理三角形三个内角的和等于180°图6-48已知,如图6-48,△ABC.求证:∠A+∠B+∠C=180°证明:作BC的延长线CD,过点C作射线CE∥BA,则:∠A=∠ACE()∠ECD=∠B() ∠ECD+∠ACE+∠ACB=180°()∴∠A+∠B+∠ACB=180°()二、议一议三、课堂练习四、课时小结五、课后作业●教学过程Ⅰ.巧设现实情境,引入新课图6-37当点A离BC越来越近时,∠A越来越接近180°,而其他两角越来越接近于0°.当点A远离BC时,∠A越来越趋近于0°,而AB与AC逐渐趋向平行,这时,∠B、∠C逐渐接近为互补的同旁内角.即∠B+∠C→180°.请同学们猜一猜:三角形的内角和可能是多少?1实验1:先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行(图6-38(1))然后把另外两角相向对折,使其顶点与已折角的顶点相嵌合(图(2)、(3)),最后得图(4)所示的结果.(1)(2)(3)(4)图6-38实验2:将纸片三角形三顶角剪下,随意将它们拼凑在一起.由实验可知:我们猜对了!三角形的内角之和正好为一个平角.但观察与实验得到的结论,并不一定正确、可靠,这样就需要通过数学证明.那么怎样证明呢?图6-39这里有两个全等的三角形,我把它们重叠固定在黑板上,然后把三角形ABC的上层∠B剥下来,沿BC的方向平移到∠ECD处固定,再剥下上层的∠A,把它倒置于∠C与∠ECD之间的空隙∠ACE的上方.这时,∠A与∠ACE能重合吗?图6-40已知:如图6-40,△ABC.求证:∠A+∠B+∠C=180°证明:作BC的延长线CD,过点C作射线CE∥AB.则∠ACE=∠A(两直线平行,内错角相等)∠ECD=∠B(两直线平行,同位角相等) ∠ACB+∠ACE+∠ECD=180°(1平角=180°)∴∠A+∠B+∠ACB=180°(等量代换)即:∠A+∠B+∠C=180°.在证明过程中,我们仅仅添画了一条射线CE,使处于原三角形中不同位置的三个角,巧妙地拼凑到一起来了.为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.我们通过推理的过程,得证了命题:三角形的内角和等于180°是真命题,这时称它为定理.即:三角形的内角和定理.2图6-41在证明三角形内角和定理时,小明的想法是把三个角“凑”到A处,他过点A作直线PQ∥BC.(如图6-41)他的想法可行吗?你有没有其他的证法. PQ∥BC(已作)∴∠PAB=∠B(两直线平行,内错角相等)∠QAC=∠C(两直线平行,内错角相等) ∠PAB+∠BAC+∠QAC=180°(1平角=180°)∴∠B+∠BAC+∠C=180°(等量代换)图6-42[生乙]也可以这样作辅助线.即:作CA的延长线AD,过点A作∠DAE=∠C(如图6-42).图6-462.如图6-46,已知,在△ABC中,DE∥BC,∠A=60°,∠C=70°,求证:∠ADE=50°.证明: DE∥BC(已知)∴∠AED=∠C(两直线平行,同位角相等) ∠C=70°(已知)∴∠AED=70°(等量代换) ∠A+∠AED+∠ADE=180°(三角形的内角和定理)∴∠ADE=180°-∠A-∠AED(等式的性质) ∠A=60°(已知)∴∠ADE=180°-60°-70°=50°(等量代换)(二)读一读P197.(三)看课本P195~196,然后小结.Ⅳ.课时小结这堂课,我们证明了一个很有用的三角形内角和定理.证明的基本思想是:运用辅助线将原三角形中处于不同位置的三个内角集中在一起,拼成一个平角.辅助线是联系命题的条件和结论的桥梁,今后我们还要学习它.Ⅴ.课后作业(一)课本P198习题6.61、2(二)1.预习内容P199~200Ⅵ.活动与探究1.证明三角形内角和定理时,是否可以把三角形的三个角“凑”到BC边上的一点P?(如图6-47(1)),如果把这三个角“凑”到三角形内一点呢?(如图6-47(2))“凑”到三角形外一点呢?(如图6-47(3)),你还能想出其他...