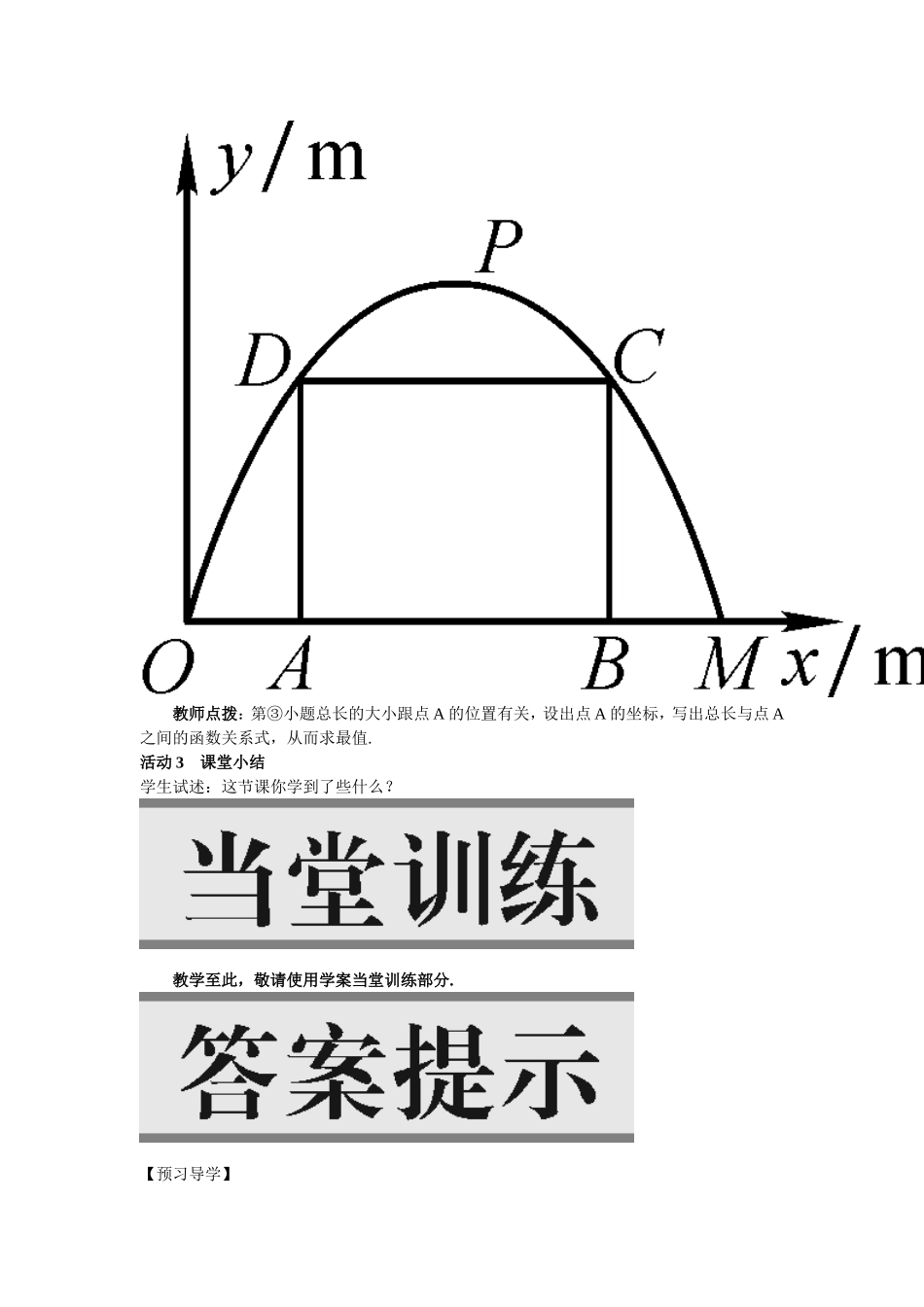
26.3实际问题与二次函数第1课时能根据实际问题建立二次函数的关系式,并探求出在何时刻,实际问题能取得理想值,增强学生解决具体问题的能力.阅读教材P22-23,自学“探究”,清楚求实际问题中的最值与二次函数最值之间的关系.自学反馈学生独立完成后集体订正①在日常生活、生产和科研中,常常会遇到求什么条件下可以使材料最省、时间最少、效率最高等问题,其中一些问题可以归结为求二次函数的最_____值或最______值.②用二次函数的知识解决实际问题时,关键是先将实际问题抽象成数学问题,即先建立_______函数关系,然后再利用________的图象及性质进行解答.③二次函数y=a(x-h)2+k中,若a>0,当x=________时,函数y有最_____值,其值为_______;若a<0,当x=________时,函数y有最________,其值为_______.教师点拨:遇到一般式,可先化成顶点式,再求最值;自变量有取值范围的还要考虑在范围内的最值.④已知二次函数y=x2-6x+m的最小值是1,那么m的值是________.教师点拨:可根据顶点公式求.⑤边长为10cm的正方形铁片,中间剪去一个边长是xcm的小正方形铁片,剩下的四方框铁片的面积y(cm2)与x(cm)之间的函数关系是.⑥某校运动会上,小明同学推出铅球时,铅球飞行的高度y(单位:m)与水平距离x(单位:m)之间的函数关系为y=x2+x+,小明同学的最好成绩是________.教师点拨:此题最好成绩是求x的最大值,而此时y=0.活动1小组讨论例1某经销店为某工厂代销一种建筑材料,当每吨售价为260元时,月销售量为45吨,该经销店为提高经营利润,准备采取降价的方式进行促销,经市场调查发现:当每吨售价下降10元时,月销售量就会增加7.5吨,综合考虑各种因素,每售出1吨建筑材料共需支付厂家及其他费用100元,设每吨材料售价为x(元),该经销店的月利润为y(元).①当每吨售价是240元时,计算此时的月销售量;②求出y与x的函数关系式(不要求写出x的取值范围);③该经销店要获得最大月利润,售价应定为每吨多少元?④小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.解:①45+×7.5=60(吨).②y=(x-100)(45+×7.5).化简,得y=x2+315x-24000.③y=x2+315x-24000=(x-210)2+9075.此经销店要获得最大月利润,材料的售价应定为每吨210元.④我认为,小静说得不对.理由:当月利润最大时,x为210元,而月销售额W=x(45+×7.5)=(x-160)2+19200当x为160元时,月销售额W最大∴当x为210元时,月销售额W不是最大的.∴小静说得不对.教师点拨:要分清利润、销售量与售价的关系;分清最大利润与最大销售额之间的区别.活动2跟踪训练(独立完成后展示学习成果)1.若抛物线y=-x2+bx+c的最高点为(-1,-3),则b=______,c=_______.教师点拨:最高点即抛物线的顶点,可根据顶点公式解此题.2.某商品的进价为每件40元,售价为每件50元,每个月可卖出210件.如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.①求y与x的函数关系式并直接写出自变量x的取值范围;②每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?③每件商品的售价定为多少元时,每个月的利润恰好为2200元?根据以上的结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元?3.如图所示,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米,现以O为原点,OM所在直线为x轴建立直角坐标系.①直接写出点M及抛物线顶点P的坐标;②求这条抛物线的解析式;③若要搭建一个矩形“支撑架”AD-DC-CB,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长的最大值是多少?教师点拨:第③小题总长的大小跟点A的位置有关,设出点A的坐标,写出总长与点A之间的函数关系式,从而求最值.活动3课堂小结学生试述:这节课你学到了些什么?教学至此,敬请使用学案当堂训练部分.【预习导学】自学反馈①大小②二次二次函数③h小kh大k10④y=-x⑤2+10010m⑥【合作探究】活动2跟踪训练1.-2-42.y=-10x①2+110x+2100(0≤x≤15)②当每件商品定价55.5元时,每个月可获得最大利润,最大的月利润...