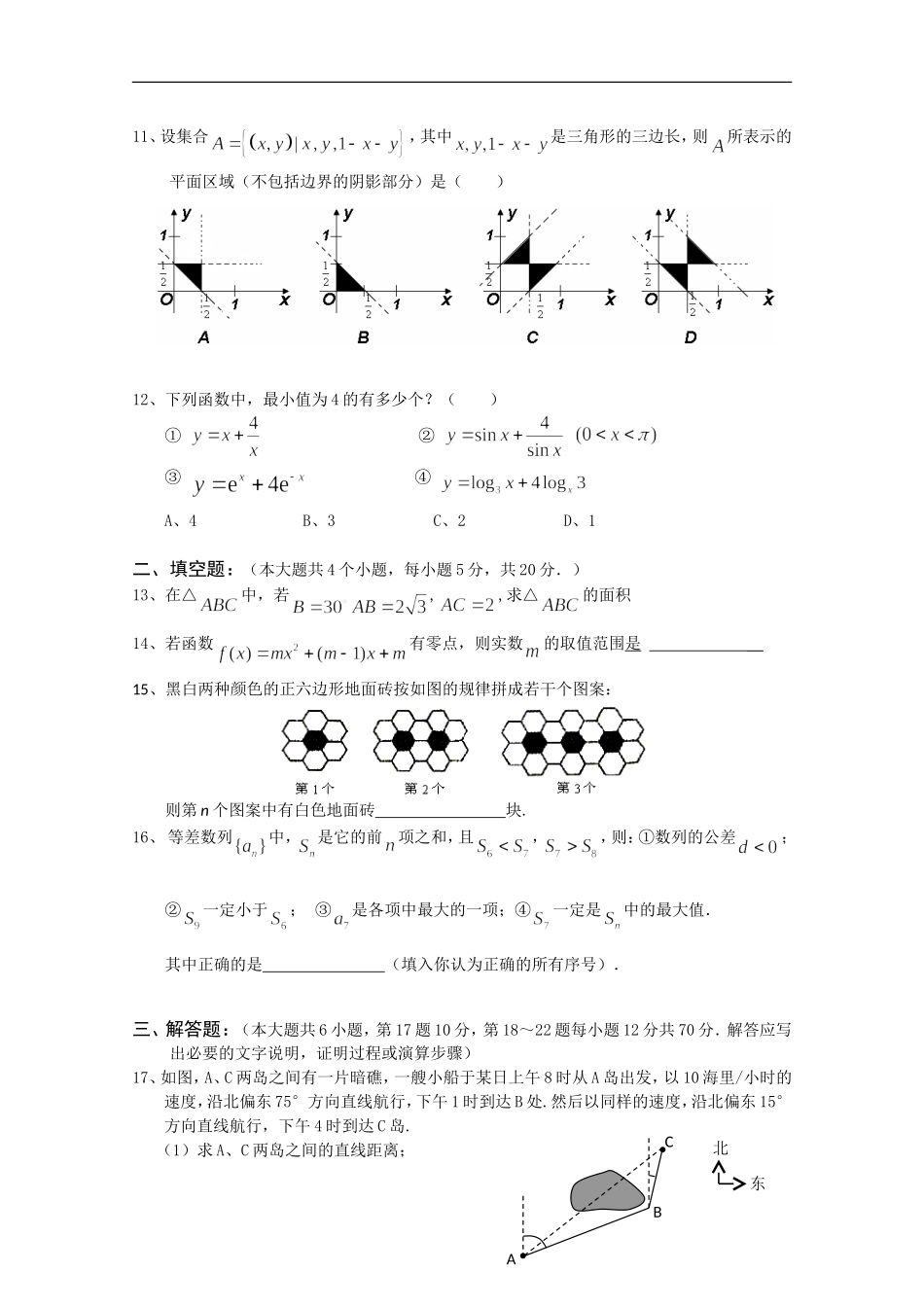
2010-2011学年度第二学期高中教学质量监测(三)高一年级数学科试题(理科)(时间:120分钟满分:150分)注意事项:1、请考生把试题卷的答案写在答题卷上,并在方框内答题,答在框外不得分;2、禁止考生使用计算器作答.一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合要求的)1、若,,则下面结论中,正确的是()A、B、C、D、2、在△中,已知,,,则()A、B、C、D、3、已知数列则是这个数列的()A、第六项B、第七项C、第八项D、第九项4、三角形三边形,且满足等式,则边所对角为()A、150°B、30°C、60°D、120°5、在等差数列中,,,则()A、48B、50C、60D、806、在等比数列中,,,则=()A、40B、70C、30D、907、不等式组的解集为()A、B、C、D、8、设等差数列的前n项之和为,已知,则()A、12B、20C、40D、1009、在△ABC中,若,则△ABC的形状是()A、直角三角形B、等边三角形C、等腰三角形D、锐角三角形10、已知数列满足,则=()A、B、0C、D、11、设集合,其中是三角形的三边长,则所表示的平面区域(不包括边界的阴影部分)是()12、下列函数中,最小值为4的有多少个?()①②③④A、4B、3C、2D、1二、填空题:(本大题共4个小题,每小题5分,共20分.)13、在△中,若,,求△的面积14、若函数有零点,则实数的取值范围是__15、黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案:则第n个图案中有白色地面砖块.16、等差数列中,是它的前项之和,且,,则:①数列的公差;②一定小于;③是各项中最大的一项;④一定是中的最大值.其中正确的是(填入你认为正确的所有序号).三、解答题:(本大题共6小题,第17题10分,第18~22题每小题12分共70分.解答应写出必要的文字说明,证明过程或演算步骤)17、如图,A、C两岛之间有一片暗礁,一艘小船于某日上午8时从A岛出发,以10海里/小时的速度,沿北偏东75°方向直线航行,下午1时到达B处.然后以同样的速度,沿北偏东15°方向直线航行,下午4时到达C岛.(1)求A、C两岛之间的直线距离;东北ABC(2)求∠BAC的正弦值.18、某种汽车购买时费用为14.4万元,每年应交付保险费、养路费及汽油费共0.9万元,汽车的维修费为:第一年0.2万元,第二年0.4万元,第三年0.6万元,……,依等差数列逐年递增.(1)设使用年该车的总费用(包括购车费用)为,试写出的表达式;(2)求这种汽车使用多少年报废最合算(即该车使用多少年平均费用最少).19、已知函数,其中为实常数.(1)当时,求不等式的解集;(2)当变化时,讨论关于的不等式的解集.20、要将两种厚度、材质相同,大小不同的钢板截成、、三种规格的成品.每张钢板可同时截得三种规格的块数如下表:成品规格类型钢板类型A规格B规格C规格第一种钢板121第二种钢板113每张钢板的面积:第一张为,第二张为.今需要、、三种规格的成品各为12、15、27块.则两种钢板各截多少张,可得所需三种规格的成品,且使所用钢板的面积最少?21、在△中,角A、B、C的对边分别为、、.且.(1)求的值;(2)若,求的最大值.22、设各项为正的数列,其前项和为,并且对所有正整数,与2的等差中项等于与2的等比中项.(1)写出数列的前二项;(2)求数列的通项公式(写出推证过程);(3)令,求的前项和.东北ABC东北ABC2010-2011学年度第二学期高中教学质量监测(三)高一年级数学科参考答案(理科)一、DDBCCABBCAAD二、13.或14.15.16.①②④三、17、解(1)在△ABC中,由已知,AB=10×5=50,BC=10×3=30,∠ABC=180°-75°+15°=120°(2分)据余弦定理,得,所以AC=70.(4分)故A、C两岛之间的直线距离是70海里.(5分)(2)在△ABC中,据正弦定理,得,(7分)所以.(9分)故∠BAC的正弦值是.(10分)18、解:(1)依题意,有(6分)(2)设该车的年平均费用为S万元,则有(10分)当且仅当,即时,等号成立.(12分)答:汽车使用12年报废为宜.19、解(1)当时,由,得,即.(2分)∴不等式的解集是,(4分)(2)由,得,即.(6分)当,即时,不等式的解集为或;(8分)当,即时,不等式的解集为或;(10分)当,即时...