江苏省2012高考数学填空题提升练习(50)-苏教版VIP免费

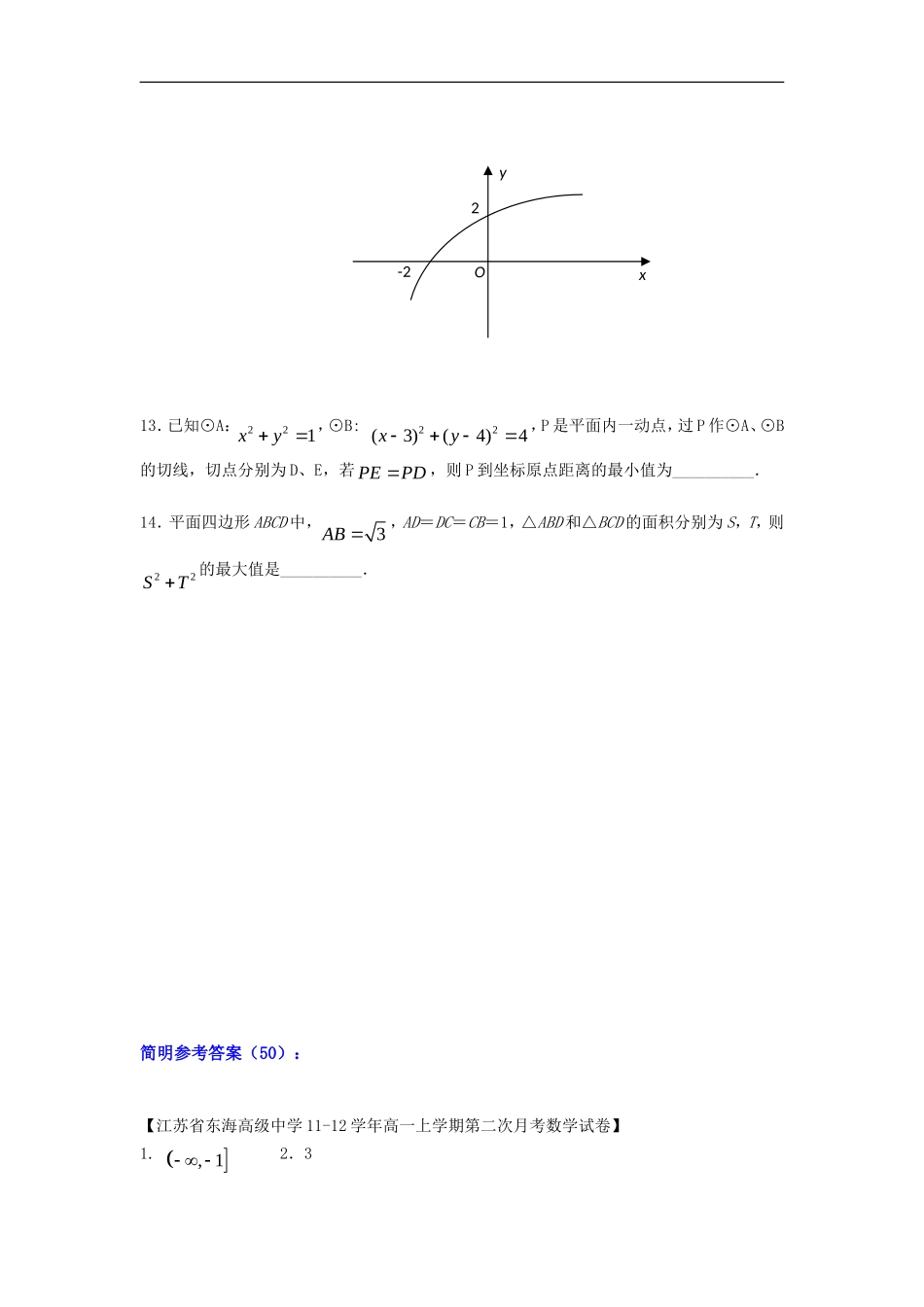
2012江苏高考数学填空题“提升练习”（50）1.已知函数2()2fxxxa和函数()21gxxx,对任意1x,总存在2x使12()()gxfx成立,则实数a的取值范围是__________．2.设函数2()()1||xfxxxR，区间[,]()Mabab，集合{|(),}NyyfxxM，则使MN成立的实数对,ab有__________对．3.已知正四棱锥的底面边长为2，体积为4，则其侧面积为__________．4.在△ABC中，D为BC的中点，AD=1，∠ADB=120o，若AB=3AC，则BC=__________．5.已知直角梯形ABCD中，AD∥BC,∠ADC=90o，AD=2，BC=1，P为腰DC上的动点，则23PAPB�的最小值为__________．6.若实数a、b、c满足lg1010abab，lg101010abcabc，则c的最大值是__________．7.对于数列｛an｝，定义数列｛bn｝、｛cn｝：bn=an+1-an，cn=bn+1-bn.若数列｛cn｝的所有项均为1，且a10=a20=0，则a30=__________．8.已知a>0,方程x2-2ax-2alnx=0有唯一解,则a=__________．9.若圆422yx上存在与点)3,2(aa距离为1的点，则a的取值范围为__________．10.在正三棱锥ABCD中，E是BC的中点，AEAD．若2BC，则正三棱锥ABCD的体积为__________．11.已知直线10kxy)0(k与圆41:22yxC相交于,AB两点，若点M在圆C上，且有OMOAOB�（O为坐标原点），则实数k=__________．12．函数log()ayxb的图象如图所示，则ab的值为__________．13．已知⊙A：221xy，⊙B:22(3)(4)4xy，P是平面内一动点，过P作⊙A、⊙B的切线，切点分别为D、E，若PEPD，则P到坐标原点距离的最小值为__________．14．平面四边形ABCD中，3AB，AD＝DC＝CB＝1，△ABD和△BCD的面积分别为S，T，则22ST的最大值是__________．简明参考答案（50）：【江苏省东海高级中学11-12学年高一上学期第二次月考数学试卷】1.,12．3xyO2-2【江苏省高考模拟练习】3～8缺答案【江苏省海门中学高二12月学情调研数学试卷】9.6,0510.2311.15【江苏省海头高级中学2012高三期末模拟数学试题二】12．3313．11514．78