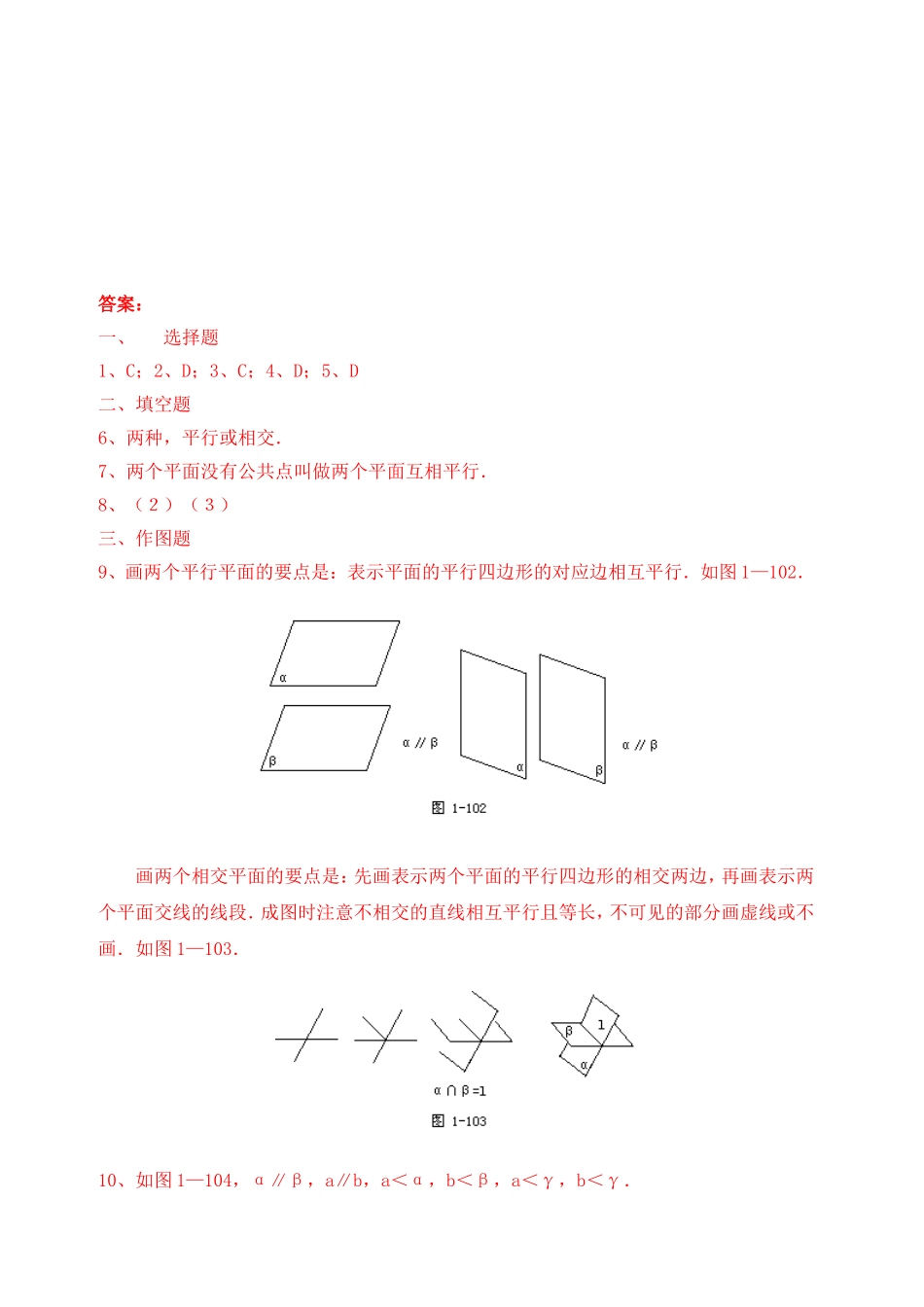
2、1、4平面与平面之间的位置关系练习一一、选择题1、设直线l、m,平面α、β,下列条件能得出α∥β的是()A、lα,mα,且l∥β,m∥β;B、lα,mβ,且l∥m;C、l⊥α,m⊥β,且l∥m;D、l∥α,m∥β,且l∥m、2、如果两个平面分别经过两条平行线中的一条,那么这两个平面()A、平行;B、相交;C、垂直;D、都有可能3、经过平面α外一条直线a与平面α平行的平面()A、有且只有一个;B、不存在C、至多有一个;D、至少有一个4、直线AB和CD分别与互相平行的三个平面α、β、γ相交于A、G、B和C、E、D,又AD和CB与β分别交于H、F,则下列结论中成立的是()A、E、F、G、H四点一定构成一个平行四边形;B、E、F、G、H四点不能构成一个平行四边形;C、E、F、G、H四点一定共线;D、E、F、G、H四点共线或构成一个平行四边形.5、与空间不共面四点距离相等的平面有()A、3个;B、4个;C、6个;D、7个二、填空题6、两个平面的位置关系可分为________________________。7、______________________________________是平行的平面。8、下列命题中:(1)平行于同一直线的两个平面平行;(2)垂直于同一直线的两个平面平行;(3)平行于同一平面的两个平面平行;(4)与同一直线成等角的两个平面平行.正确命题的序号是.三、作图题9、那么如何画出并表示两个平行平面和两个相交平面呢?10、画两个平行平面和分别在这两个平面内的两条平行直线,再画一个经过这两条平行直线的平面.四、判断题11、垂直于同一直线的两直线平行.12、分别在两个平行平面内的两条直线都平行.13、如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行.14、如果一个平面内的任何一条直线都平行于另一个平面,那么这两个平面平行五、解答题15、已知:如图2.2.4-1,α∥β,AB∥CD,A∈α,C∈α,B∈β,D∈β.求证:AB=CD.答案:一、选择题1、C;2、D;3、C;4、D;5、D二、填空题6、两种,平行或相交.7、两个平面没有公共点叫做两个平面互相平行.8、(2)(3)三、作图题9、画两个平行平面的要点是:表示平面的平行四边形的对应边相互平行.如图1—102.画两个相交平面的要点是:先画表示两个平面的平行四边形的相交两边,再画表示两个平面交线的线段.成图时注意不相交的直线相互平行且等长,不可见的部分画虚线或不画.如图1—103.10、如图1—104,α∥β,a∥b,a<α,b<β,a<γ,b<γ.四、判断题11、错,这两条直线还可能相交或异面.12、错,这两条直线还可能异面,但不会相交.13、错,反例如图1—107.14、对.五、解答题15、证明:∵AB∥CD,∴过AB、CD的平面γ与平面α和β分别交于AC'和BD.∵α∥β,∴BD∥AC.∴四边形ABCD是平行四边形,∴AB=CD.