直线与双曲线的位置关系VIP免费

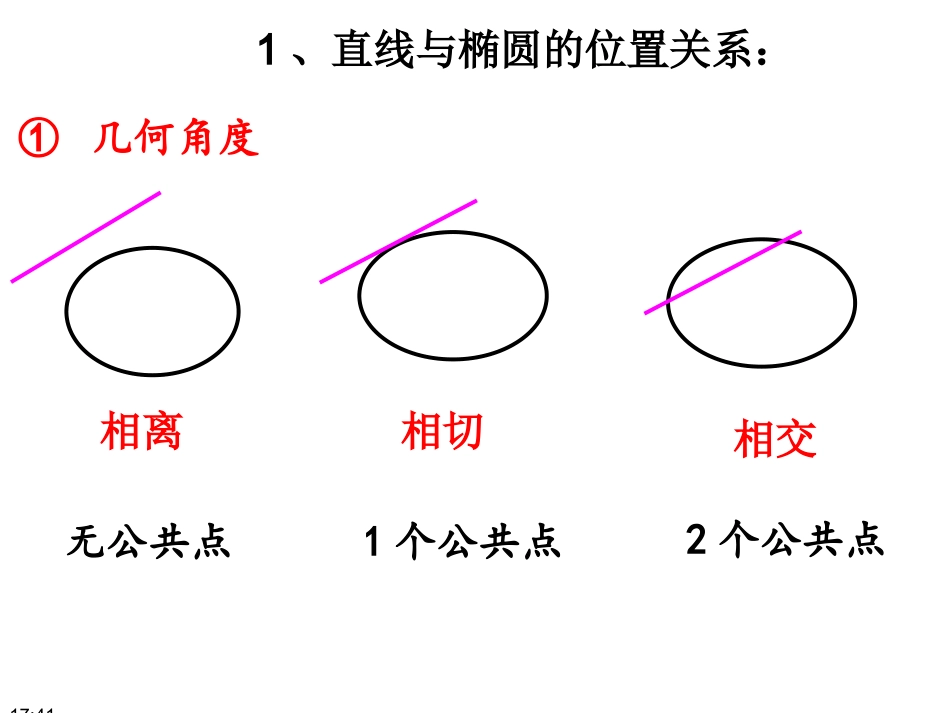
直线与双曲线的位置关系17:41复习回顾：1、直线与椭圆的位置关系：相离相交相切无公共点1个公共点2个公共点①几何角度17:41设直线与椭圆方程分别为设直线与椭圆方程分别为::(1)(1)>0△>0△⇔相交相交(2)(2)△=0△=0相切相切(3)(3)△<0△<0相离相离ykxm222210,0xyabab联立方程组联立方程组::22221ykxmxyab消消((或或))得：得：yx②代数角度2222222220bakxkmaxamb1、直线与椭圆的位置关系：17:41直线绕着点(0，2)旋转过程中，与双曲线的位置关系如何？交点个数情况如何？224xyl探究1：（1）相离（3）相交（2）相切无交点2个交点或1个交点1个交点直线与双曲线的位置关系：-22xy2o0l1l2l3l4l17:41位置关系与交点个数xyOxyO相离:0个交点相交:2个交点相切:1个交点特殊的相交(与渐近线平行)：1个交点17:41(2)相离(3)有2个公共点(5)与右支相交于2点(4)交于异支2点例1：直线与双曲线满足下列条件时，分别求出直线的斜率的值或范围？224xy:2lykxlk22k且1k2k2k或11k(1)有1个公共点1k2k或直线与双曲线的位置关系的判断2-1k17:411个交点相切0个交点2个交点相离相交0002.二次项系数不为0时,上式为一元二次方程,22221ykxmxyab2222222220bakxkmaxamb消得：y1.二次项系数为0时，与双曲线的渐近线平行或重合。l(平行：1个交点；重合：无交点)直线与双曲线的位置关系的判断17:41相交两点:①交于异支（异侧）：120xx②与右支交于2点（同侧）：121200xxxx③与左支交于2点（同侧）：121200xxxx22200bak22221ykxmxyab2222222220bakxkmaxamb消得：y17:41(2)相离(3)有2个公共点(5)与右支相交于2点(4)交于异支2点例1：直线与双曲线满足下列条件时，分别求出直线的斜率的值或范围？224xy:2lykxlk22k且1k2k2k或11k(1)有1个公共点1k2k或直线与双曲线的位置关系的判断2-1k17:414例2：过点P(0,2)与双曲线只有一个交点的直线共有_____条.224xy-22xy2o1l2l3l4l17:41练习:将点A(2,2)改为2变式：过点A(2,2)与双曲线只有一个交点的直线共有____条.3条2条0条(1)B(2,0)(2)C(3,0)(3)D(0,0)224xy答案又是怎样的?-22xyoyx-yxA2归纳：过一定点与双曲线仅有一个交点的直线条数的判断—数形结合，相切或与渐近线平行。012k0变题1:若直线与双曲线有两个相异公共点，求的范围.1kxy422yxk55(,1)(1,1)(1,)22k的取值范围22x-y=422(1-k)x+2kx-5=0要使直线与双曲线的右支有两个相异的公共点，则应满足解：将直线代入双曲线方程1kxy052)1(22kxxk化简整理422yx（※）变题2:若直线与双曲线的右支有两个相异公共点，求的范围.422yxk1kxy251k解得2212121210010()4002()40kkxxxxxx注:直线与双曲线的右支有两个交点,实际上给出了方程解的范围,涉及到二次方程的根的分布问题.解题时需要注意!12120.0xxxx想一想?1212(2)(2)0(2)(2)0xxxx17:41走向高考.3,3,.3,3,2,2,2,2ABCD曲线总有公共点，则b的取值范围是（）2ykxb221xy若不论k为何值，直线与17:41回顾与小结分类讨论思想,数形结合思想一、主要知识三、思想与方法1.直线与双曲线的位置关系。2.直线与双曲线的公共点个数。二、重点判断直线与双曲线的位置关系代数法几何法17:41判断直线与双曲线位置关系的操作程序：把直线方程代入双曲线方程得到一元一次方程得到一元二次方程直线与双曲线的渐近线平行相交（一个交点）计算判别式>0=0<0相交相切相离归纳归纳17:41特别注意直线与双曲线的位置关系中：一解不一定相切，相交不一定两解，两解不一定同支