一元二次方程VIP免费

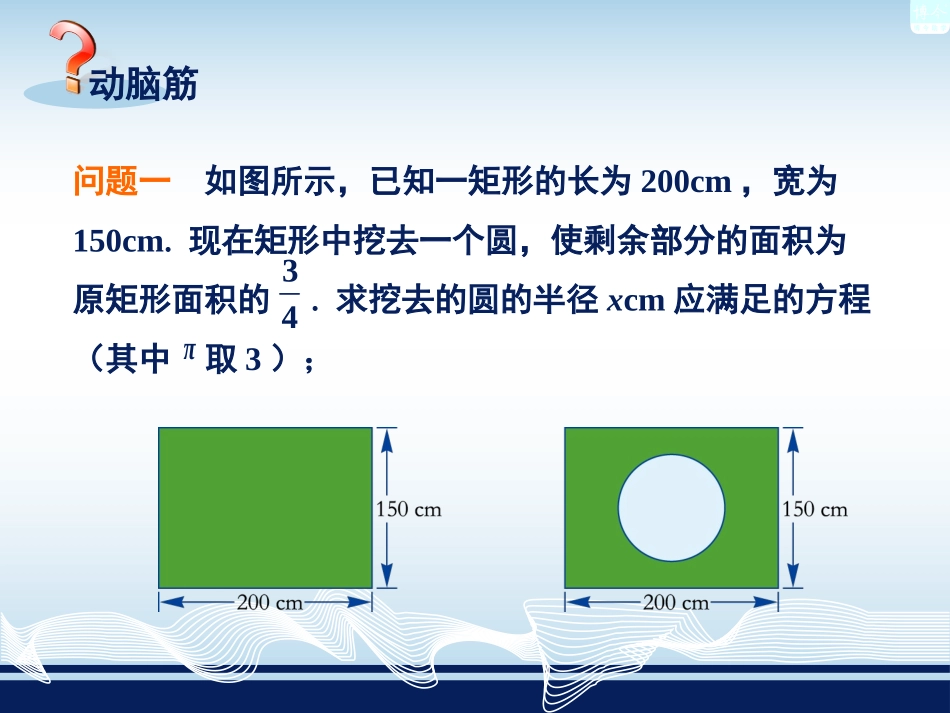
第2章一元二次方程第1课一元二次方程的概念一元二次方程第2章动脑筋问题一如图所示，已知一矩形的长为200cm，宽为150cm.现在矩形中挖去一个圆，使剩余部分的面积为原矩形面积的.求挖去的圆的半径xcm应满足的方程（其中取3）；34π问题二据某市交通部门统计，前年该市汽车拥有量为75万辆，两年后增加到108万辆．求该市两年来汽车拥有量的年平均增长率x应满足的方程．问题一、二涉及的等量关系分别是：矩形的面积-圆的面积=矩形的面积×.两年后的汽车拥有量=前年的汽车拥有量×（1+年平均增长率）2.问题一、二涉及的等量关系分别是：矩形的面积-圆的面积=矩形的面积×.两年后的汽车拥有量=前年的汽车拥有量×（1+年平均增长率）2.34要建立方程，关键是找出问题中的等量关系.解由于圆的半径为xcm，则它的面积为3x2cm2．根据等量关系，可以列出方程200×150-3x2=.32001504225000x①化简，整理得问题一如图所示，已知一矩形的长为200cm，宽为150cm.现在矩形中挖去一个圆，使剩余部分的面积为原矩形面积的.求挖去的圆的半径xcm应满足的方程（其中取3）；34π解该市两年来汽车拥有量的年平均增长率为x．25x2+50x-11=0．②化简，整理得根据等量关系，可以列出方程75（1+x）2=108.问题二据某市交通部门统计，前年该市汽车拥有量为75万辆，两年后增加到108万辆．求该市两年来汽车拥有量的年平均增长率x应满足的方程．说一说方程①②中有几个未知数？它们的左边是x的几次多项式？225000x①25x2+50x-11=0．②从方程①和②中受到启发，如果一个方程通过整理可以使右边为0，而左边是只含有一个未知数的二次多项式，那么这样的方程叫作一元二次方程.满足：1、一个未知数2、含有未知数项的最高次数为23、整式方程结论结论它的一般形式是ax2+bx+c=0（a，b，c是已知数，a≠0）ax2+bx+c=0（a，b，c是已知数，a≠0）其中a，b，c分别叫作二次项系数、一次项系数、常数项．例如方程x2-2500=0中二次项系数是1，一次项系数是0，常数项是-2500.例题典析例1下列方程是否为一元二次方程？若是，指出其中的二次项系数、一次项系数和常数项.（1）3x（1-x）+10=2（x+2）；（2）5x（x+1）+7=5x2-4.（1）3x（1-x）+10=2（x+2）这是一元二次方程，其中二次项系数是-3，一次项系数是1，常数项是6.解去括号，得3x-3x2+10=2x+4，移项，合并同类项，得-3x2+x+6=0，（2）5x（x+1）+7=5x2-4去括号，得5x2+5x+7=5x2-4.解移项，合并同类项，得5x+11=0，这是一元一次方程，不是一元二次方程.练习1.请用线把左边的方程与右边所对应的方程类型连接起来：2x2+5x=x2-3（x+1）2-1=x2+43x+5=2x–1一元一次方程一元二次方程分式方程x12=x32.下列方程是否为一元二次方程？若是，指出其中的二次项系数、一次项系数和常数项．（1）4x2=49；（2）式是一元二次方程，二次项系数是5，一次项系数是-3，常数项是-2;答：（1）式是一元二次方程，二次项系数是4，一次项系数是0，常数项是-49;（2）5x2-2=3x；（4）式不是一元二次方程.（3）0.01t2=2t；（4）（9y-1）（2y+3）=18y2+1.（3）式是一元二次方程，二次项系数是0.01，一次项系数是-2，常数项是0;答：例2（补例）一元二次方程3x2+x-2=0的二次项系数和常数项分别为（）.A.3，1B.-1，-2C.3，-2D.-1，2由一般形式ax2+bx+c=0(a≠0)，得a=3，c=-2.故选择C.解C例3（补例）将方程3x2=5x+2化为一元二次方程的一般形式是：.3x2-5x-2=0作业布置课本第28页习题2.1A组第1题