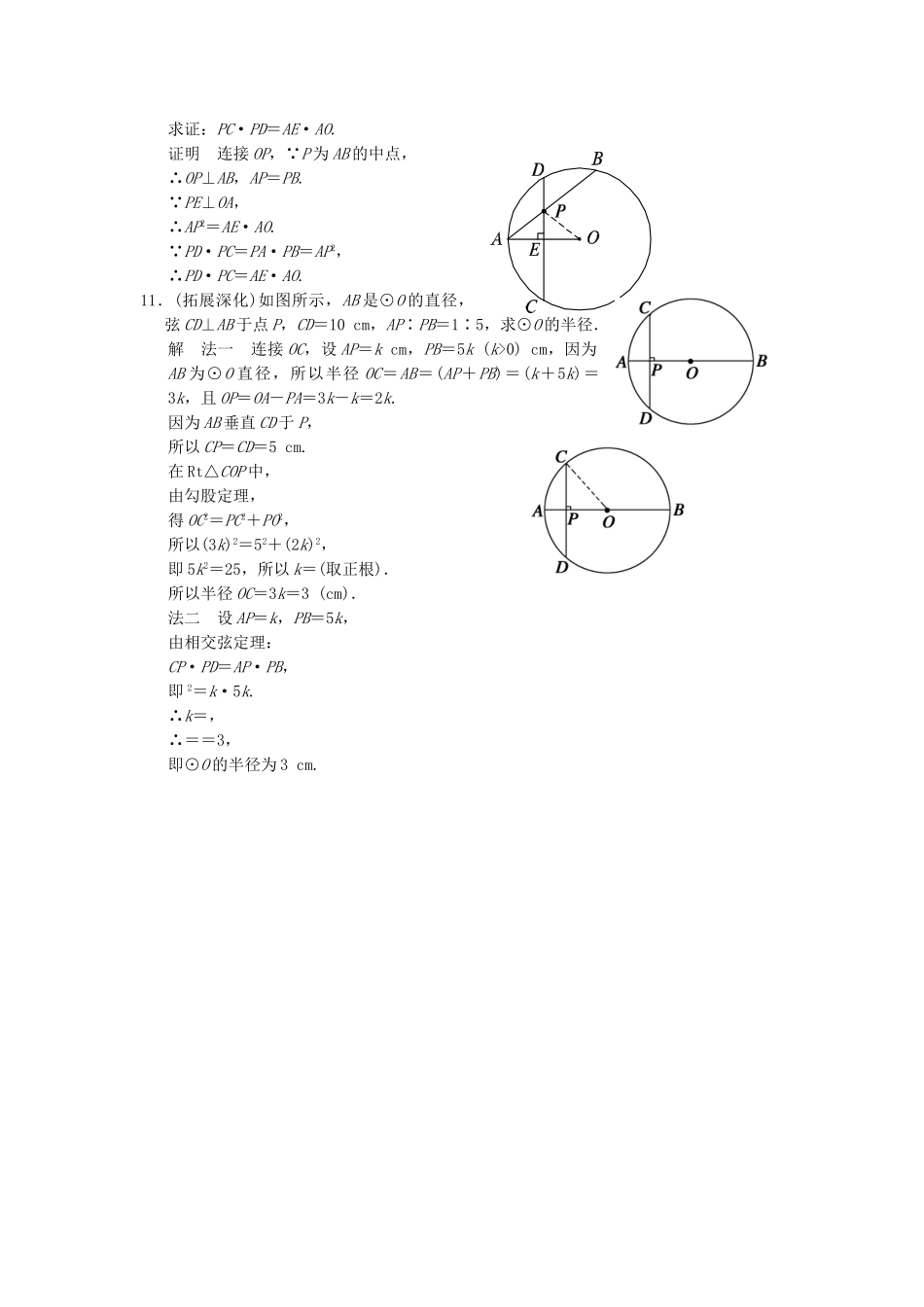
【创新设计】届高考数学2-5与圆有关的比例线段知能演练新人教A版选修4-1一、选择题1.如图所示,PC切⊙O于A,PO的延长线交⊙O于B,BC切⊙O于B,若AC∶CP=1∶2,则PO∶OB等于().A.2∶1B.1∶1C.1∶2D.1∶4解析在题图中连接OA,则OA⊥PC,∴△PAO∽△PBC,∴=,即=,又∵OA=OB,AC∶CP=1∶2,设AC=x,则CP=2x,∴CA=x=BC,∴==2,∴PO∶OB=2∶1.答案A2.如图所示,PA、PB是⊙O的两条切线,A、B为切点,连接OP交AB于C,连接OA、OB,则图中等腰三角形、直角三角形个数分别为().A.1,2B.2,2C.2,6D.1,6解析∵PA、PB为⊙O切线,∴OA⊥AP,OB⊥PB,PA=PB,OP平分∠APB,∴OP⊥AB.∴直角三角形有6个,等腰三角形有2个.即直角三角形有:△OAP,△OBP,△OCA,△OCB,△ACP,△CBP;等腰三角形有:△OAB,△ABP.答案C3.圆内两条相交弦,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1∶4两部分,则这条弦长是().A.2cmB.8cmC.10cmD.12cm解析由相交弦推论即可得.设另一条弦被分成xcm,4xcm.则2=x·4x,所以x=2cm.所以弦长为10cm.答案C4.如图所示,在⊙O中,弦AB与半径OC相交于点M,且OM=MC,AM=1.5,BM=4,则OC等于().A.2B.C.2D.2解析延长CO交⊙O于D,则DM=3CM,CM·MD=MA·MB,所以1.5×4=3CM2,CM=,OC=2.答案D二、填空题5.如图所示,已知⊙O的两条弦AB、CD相交于AB的中点E,且AB=4,DE=CE+3,则CD的长为________.解析由相交弦定理知EA·EB=EC·ED.(*)又∵E为AB中点,AB=4,DE=CE+3,∴(*)式可化为22=EC(CE+3)=CE2+3CE,∴CE=-4(舍去)或CE=1.∴CD=DE+CE=2CE+3=2+3=5.答案56.如图所示,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于点D、E,交AB于点C,图中互相垂直的线段有________⊥________.(只要求写出一对线段)解析如题图所示,由于PA、PB均为⊙O切线,∴PA⊥OA,PB⊥OB.又由切线长定理知PA=PB,OP为∠APB的角平分线,∴AB⊥OP,故应填PA⊥OA或PB⊥OB或AB⊥OP.答案ABOP7.如图所示,AB为⊙O的直径,CB切⊙O于B,CD切⊙O于D,交BA的延长线于E,若EA=1,ED=2,则BC的长为________.解析∵CE为⊙O切线,D为切点,∴ED2=EA·EB.又∵EA=1,ED=2,∴EB=4,又∵CB、CD均为⊙O切线,∴CD=CB.在Rt△EBC中,设BC=x,则EC=x+2.由勾股定理:EB2+BC2=EC2得42+x2=(x+2)2,得x=3,∴BC=3.答案38.已知PAB、PCD是⊙O的两条割线,PC=AB,PA=20,CD=11,则AB的长为________.解析设PC=AB=x,则x(x+11)=20×(20+x),解得x=25.所以AB的长为25.答案25三、解答题9.如图所示,四边形ABCD的边AB、BC、CD、DA和⊙O分别相切于点L、M、N、P.求证:AB+CD=AD+BC证明因为AB、BC、CD、DA都与⊙O相切,L、M、N、P为切点,所以AL=AP,LB=MB,DN=DP,NC=MC.所以AB+CD=AL+LB+DN+NC=AP+MB+DP+MC=AD+BC.即AB+CD=AD+BC.10.如图,已知在⊙O中,P是弦AB的中点,过点P作半径OA的垂线分别交⊙O于C、D两点,垂足是点E.求证:PC·PD=AE·AO.证明连接OP,∵P为AB的中点,∴OP⊥AB,AP=PB.∵PE⊥OA,∴AP2=AE·AO.∵PD·PC=PA·PB=AP2,∴PD·PC=AE·AO.11.(拓展深化)如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP∶PB=1∶5,求⊙O的半径.解法一连接OC,设AP=kcm,PB=5k(k>0)cm,因为AB为⊙O直径,所以半径OC=AB=(AP+PB)=(k+5k)=3k,且OP=OA-PA=3k-k=2k.因为AB垂直CD于P,所以CP=CD=5cm.在Rt△COP中,由勾股定理,得OC2=PC2+PO2,所以(3k)2=52+(2k)2,即5k2=25,所以k=(取正根).所以半径OC=3k=3(cm).法二设AP=k,PB=5k,由相交弦定理:CP·PD=AP·PB,即2=k·5k.∴k=,∴==3,即⊙O的半径为3cm.