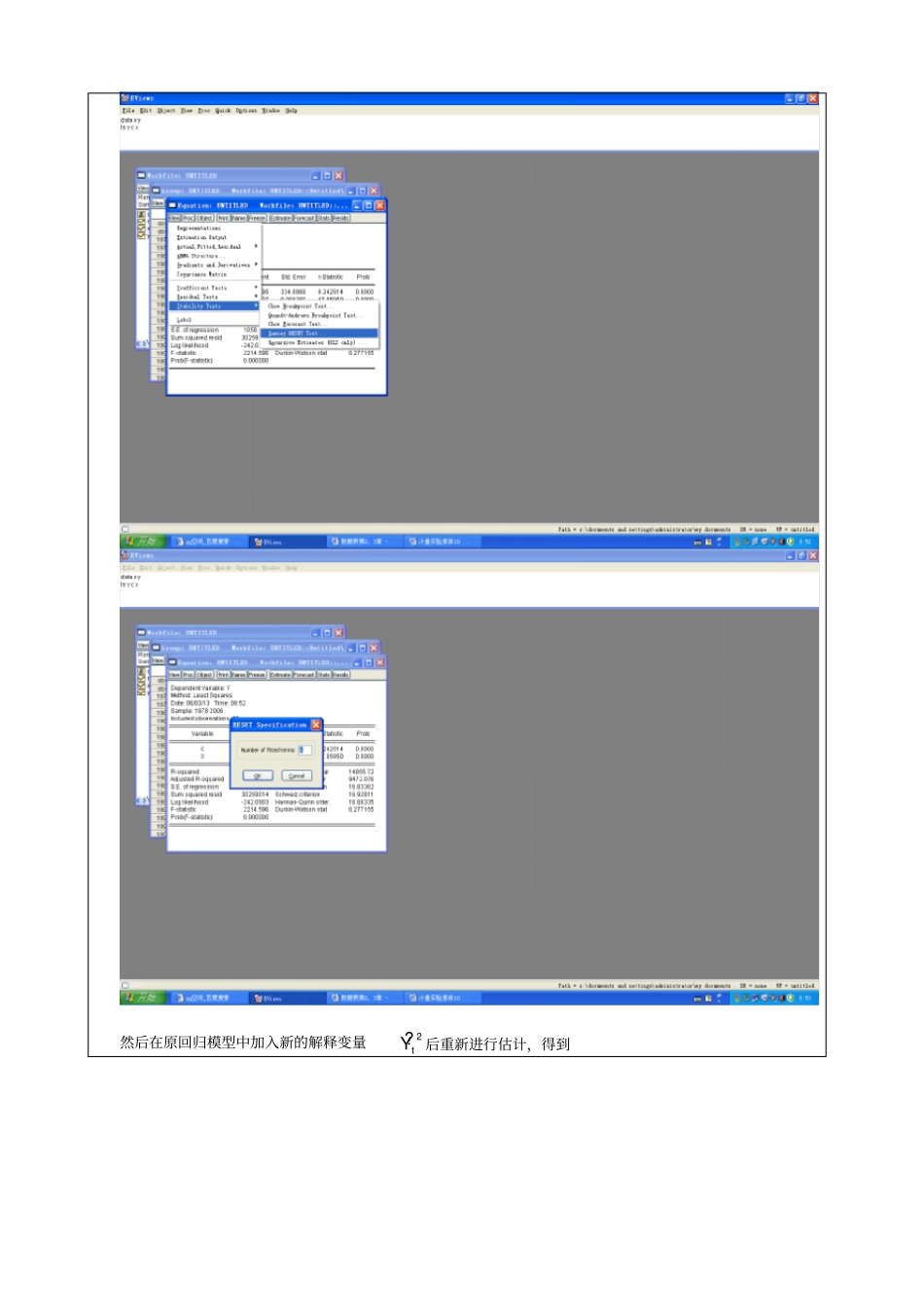
计量经济学实验报告10学号班级10707姓名实验时间2013.6.3实验序号10实验名称格兰杰与拉姆齐检验开设实验室经济学实验室实验目的:掌握格兰杰与拉姆齐检验的原理与方法。实验内容:1、格兰杰检验的原理与方法;2、拉姆齐检验的原理与方法。3、练习教材P176例5.2.4、P183例5.3.1实验报告(1、实验操作过程;2、实验结果;3、对实验结果的分析或体会):例5.3.1建立工作表,输入数据,对原模型进行最小二乘估计,点击enter则出现然后进行RESET检验,操作如下:点击ViewStabilityTestsRamseyResetTest则出现然后在原回归模型中加入新的解释变量2t?Y后重新进行估计,得到原回归模型的可决系数为2R=0.9880.计算F统计量:(0.99530.9880)/140.3(10.9953)/(293)F该值大于5%的显著性水平下、自由度为(1,26)的F分布临界值4.22,因此拒绝原模型与引入新变量的模型可决系数无显著差异的假设,表明原模型确实存在遗漏相关变量的设定偏误。为了将Y与X随时间共同变化的时间趋势因素分离出来,模型引入了时间趋势项2T,并通过普通最小二乘法估计了二元回归模型得到如下:在命令窗口输入genrt=@trend(1977),再输入lsycxt^2点击enter即可为了确定该模型是否是一正确的模型,仍进行RESET检验,由该模型计算的消费总量序列记为??tY并将它的平方项作为解释变量加入该二元模型中进行普通最小二乘估计得,原二元回归模型的可决系数为2R=0.997590,计算F统计量为(0.9976260.997590)/10.38(10.997626)/(294)F,该值小于5%的显著性水平下,自由度为(1,25)的F分布的临界值4.24,表明加入时间趋势项2T的总量消费模型已不存在设定偏误问题,同样,通过再引入??tY的立方项后仍可验证原模型不存在设定偏误问题。例5.2.4依据中国1978—2006年的数据,建立工作表,输入数据,输入命令LSYCX(-1)Y(-1),进行XY格兰杰因果性检验取出AIC值,点击enter则出现对上述结果做LM检验记录LM(1)检验的P值输入命令LSXCX(-1)Y(-1),进行YX格兰杰因果性检验取出AIC值,点击enter则出现同样对上述结果进行LM检验记录LM(1)检验的P值从检验模型随机干扰项1阶序列相关的拉格朗日乘数检验看,以Y为被解释变量的模型的LM检验的P值为0.3895,表明在5%的显著性水平下,该模型不存在序列相关性。但是以X为被解释变量的模型的LM检验的P值0.0015,表明在5%的显著性水平下,该模型存在严重的序列相关性。重复如上操作,分别作出滞后2到4阶的AIC值和LM1阶检验在数组窗口点击view中的grangercausality进行滞后1阶的X与Y的格兰杰因果关系检验得到居民消费与收入间的格兰杰因果关系如下图由伴随概率知,在5%的显著性水平下,既拒绝“X不是Y的格兰杰原因”的假设,也拒绝“Y不是X的格兰杰原因”的假设。因此从一阶滞后情况看,可支配收入X的增长与居民消费支出Y的增长互为格兰杰原因。点击view中的grangercausality分别进行滞后2—4阶的X与Y的格兰杰因果关系检验给出取1—4阶滞后的检验结果如下表中国可支配收入x与居民消费支出y的格兰杰因果关系检验滞后长度格兰杰因果性F检验的P值LM(1)检验的P值AIC值结论1XY0.00070.389514.48拒绝YX0.01850.001516.98拒绝2XY0.01260.109414.64拒绝YX0.33540.580116.688不拒绝3XY0.02460.195014.69拒绝YX0.37320.255216.82不拒绝4XY0.02960.97414.75拒绝YX0.46700.006516.97不拒绝“”表示箭头前的变量不是箭头后变量的格兰杰原因由结果看出,从2阶滞后期开始,检验模型都拒绝了“X不是Y的格兰杰原因”假设,而不拒绝“Y不是X的格兰杰原因”的假设。滞后阶数为2或3时,根据两类检验模型都不存在序列相关性,再由赤池信息准则,发现滞后2阶检验模型拥有较小的AIC值,因此,可判断可支配收入X是居民消费支出Y的格兰杰原因,而不是相反,即国民收入的增加更大程度影响着消费的增加。成绩评定:教师签名:年月日