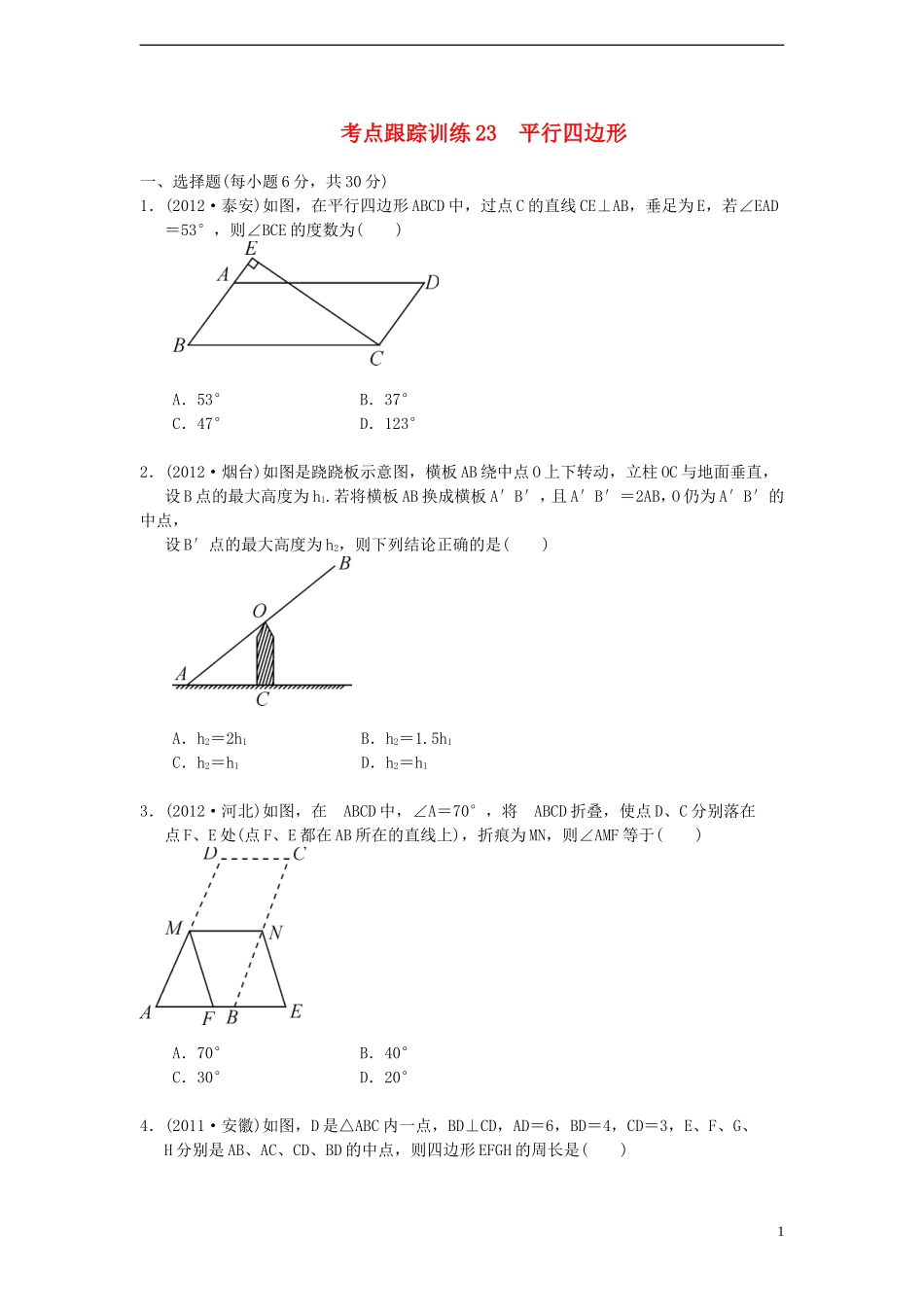
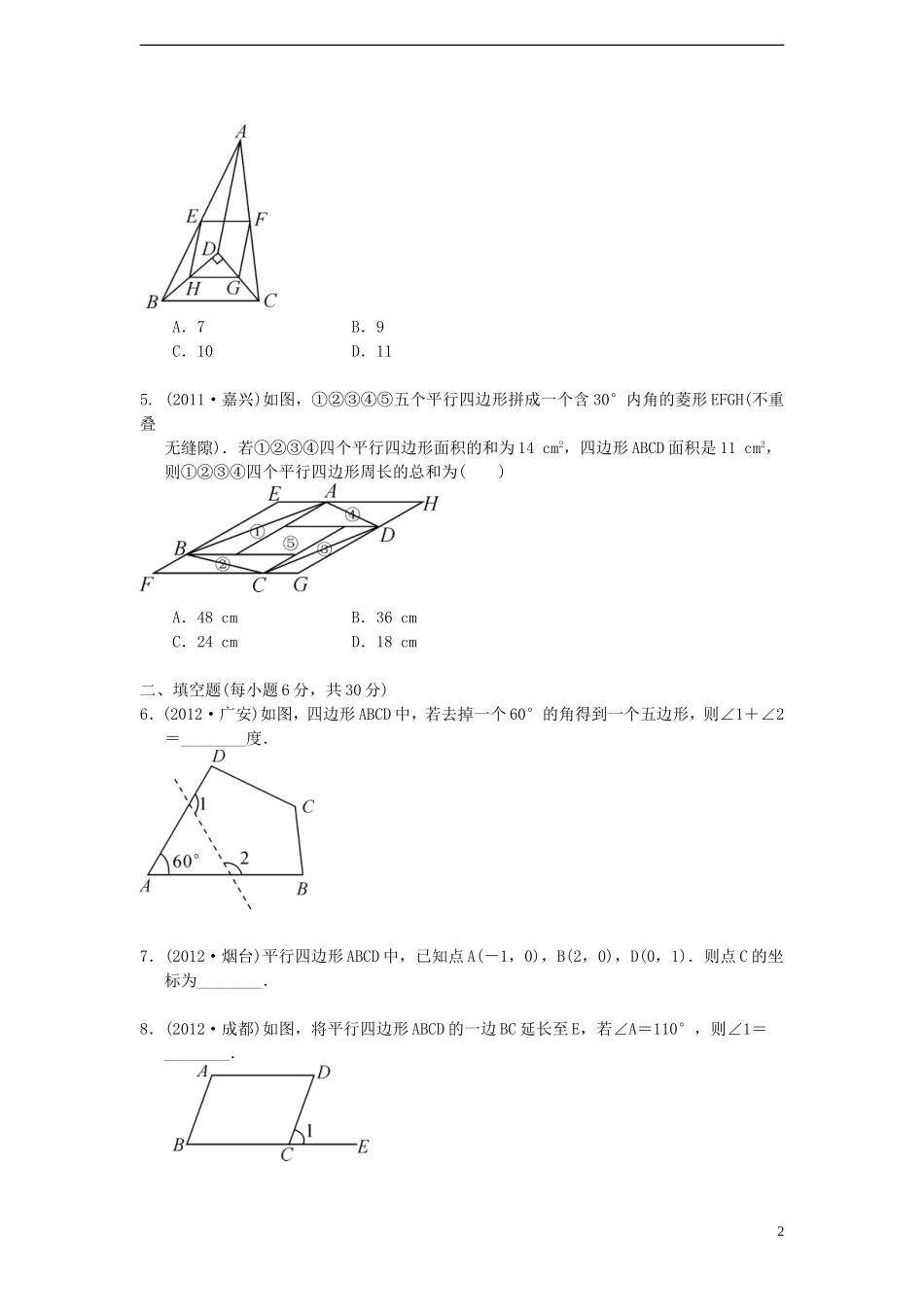
考点跟踪训练23平行四边形一、选择题(每小题6分,共30分)1.(2012·泰安)如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=53°,则∠BCE的度数为()A.53°B.37°C.47°D.123°2.(2012·烟台)如图是跷跷板示意图,横板AB绕中点O上下转动,立柱OC与地面垂直,设B点的最大高度为h1.若将横板AB换成横板A′B′,且A′B′=2AB,O仍为A′B′的中点,设B′点的最大高度为h2,则下列结论正确的是()A.h2=2h1B.h2=1.5h1C.h2=h1D.h2=h13.(2012·河北)如图,在ABCD中,∠A=70°,将ABCD折叠,使点D、C分别落在点F、E处(点F、E都在AB所在的直线上),折痕为MN,则∠AMF等于()A.70°B.40°C.30°D.20°4.(2011·安徽)如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是()1A.7B.9C.10D.115.(2011·嘉兴)如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,则①②③④四个平行四边形周长的总和为()A.48cmB.36cmC.24cmD.18cm二、填空题(每小题6分,共30分)6.(2012·广安)如图,四边形ABCD中,若去掉一个60°的角得到一个五边形,则∠1+∠2=________度.7.(2012·烟台)平行四边形ABCD中,已知点A(-1,0),B(2,0),D(0,1).则点C的坐标为________.8.(2012·成都)如图,将平行四边形ABCD的一边BC延长至E,若∠A=110°,则∠1=________.29.(2012·德阳)如图,点D、E分别是△ABC的边AB、AC的中点,连接DE,若DE=5,则BC=________.10.(2012·德州)在四边形ABCD中,AB=CD,要使四边形ABCD是中心对称图形,只需添加一个条件,这个条件可以是________________________.(只要填写一种情况)三、解答题(每小题10分,共40分)11.(2012·丽水一模)如图,已知平行四边形ABCD中,点E为BC边的中点,延长DE、AB相交于点F.求证:CD=BF.12.(2012·南安)如图,E、F是平行四边形ABCD对角线AC上的两点,且AE=CF.求证:△ADF≌△CBE.313.(2012·孝感)我们把依次连接任意一个四边形各边中点得到的四边形叫做中点四边形.如图,在四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,依次连接各边中点得到的中点四边形EFGH.(1)这个中点四边形EFGH的形状是________;(2)请证明你的结论.14.(2011·北京)在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.(1)在图1中,证明:CE=CF;(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.4四、附加题(共20分)15.(2012·广州)如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).(1)当α=60°时,求CE的长;(2)当60°<α<90°时,①是否存在正整数k,使得∠EFD=k∠AEF?若存在,求出k的值;若不存在,请说明理由;②连接CF,当CE2-CF2取最大值时,求tan∠DCF的值.5