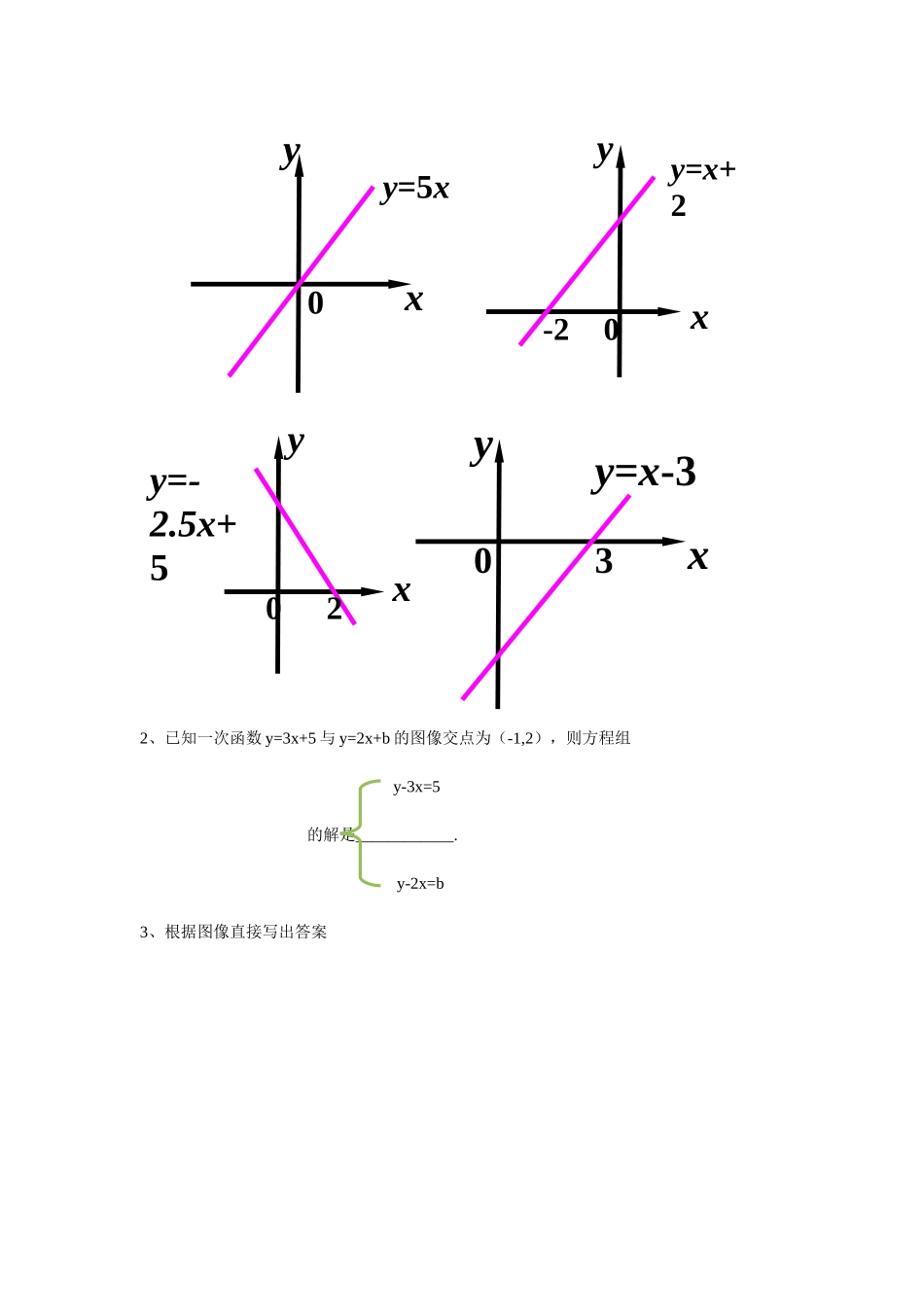
19.2.3一次函数与方程、不等式(1)学习目标:1、理解一次函数与方程(组)的关系,会根据图象解决方程(组)求解问题。2、学习用函数的观点看待方程(组)的方法,经历方程与函数关系问题的探究过程,学习用联系的观点看待数学问题。学习重点:利用一次函数图像求一元一次方程、二元一次方程组的解,并解决简单的实际问题。学习难点:一次函数与一元一次方程,二元一次方程结合解决实际问题。学习过程:一、温故知新:1、解方程:2x+20=02、解方程组:3、对于方程3x+5y=8,如何用x表示y?4、对于函数中的两个变量和,我们可以从哪些方面理解它们的含义呢?函数的表示方法有哪些?变量名称xy平面直角坐标系x轴y轴坐标系中的点横坐标纵坐标函数解析式自变量函数变量二、新知探究1、一次函数与一元一次方程:思考:下面3个方程有什么共同点和不同点?你能从函数的角度对解这3个方程进行解释吗?,,1)解这3个方程相当于在一次函数的函数值分别为3,0,-1时,求自变量x的值。2)画出的图像,从图像上可以看出上纵坐标分别取3,0,-1的点,对应的横坐标为、、归纳:1)、求一元一次方程的解相当于在一次函数2)一元一次方程的解就是直线与轴的交点的练习:作出函数y=2x+20的图像,说出它与x轴的交点坐标;说出方程2x+20=0的解。解:函数图像如图:直线y=2x+20与x轴的交点坐标为()3x+5y=82x-y=1∴方程2x+20=0的解为________。2、一次函数与二元一次方程组1号探测气球从海拔5米处出发,以1米/分的速度上升。于此同时,2号探测气球从海拔15米出发,以0.5米/分的速度上升,两个气球都上升了1小时。(1)、用式子分别表示两个气球所在的位置的海拔y(单位:米)关于上升时间x(单位:小时)的函数关系式;解:气球1海拔高度:气球2海拔高度:(2)、在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?从数的角度看:从形的角度看:归纳:从函数的观点看解二元一次方程组:1).从“数”的角度看:解方程组相当于求为何值时,两个相等,以及这个函数值是。2)从“形”的角度看:解方程组相当于确定两条直线的练习:用图像法解方程组:2x+y=4①2x-3y=12②解:由①得:由②得:作出图像:观察图像得:交点为()∴方程组的解为三、达标检测:1、根据图像,请写出图像所对应的一元一次方程的解。2、已知一次函数y=3x+5与y=2x+b的图像交点为(-1,2),则方程组y-3x=5的解是____________.y-2x=b3、根据图像直接写出答案y=5x0xyy=x+2-20xy2y=-2.5x+50xy3y=x-3x0y8642-2-4-6-8-10-5510xoyy=-2x+4y=x-423