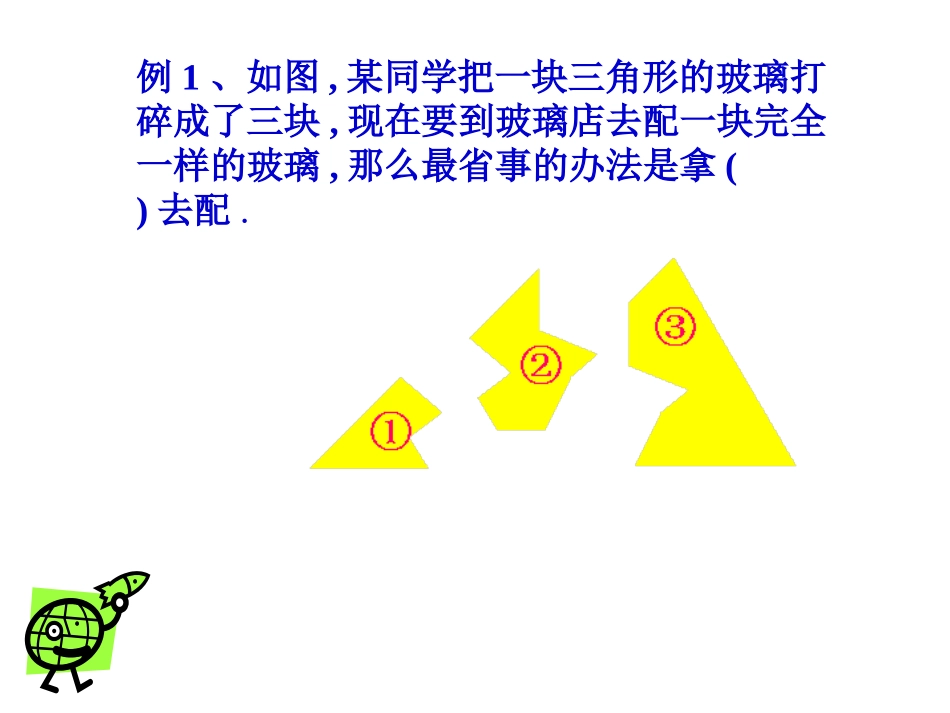
三角形全等复习乐山高新区实验中学罗毅知识点1、全等三角形的定义:能够完全重合的两个三角形叫做全等三角形2、全等三角形的性质:全等三角形的对应边相等,对应角相等。3、三角形全等的条件:SSSSASASAAASHL4、应用:利用全等三角形性质证明两条线段或两个角相等。例1、如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是拿()去配.例例22::已知已知::如图如图∠∠B=DEF,BC=EF∠B=DEF,BC=EF∠,,补充条件求证补充条件求证:ΔABC≌:ΔABC≌ΔDEFΔDEFDDEEFFAABBCC(1)(1)若要以若要以““SASSAS””为依据,还缺条件为依据,还缺条件__________;;AB=DE(2)(2)若要以若要以““ASAASA””为依据,还缺条件____;为依据,还缺条件____;∠ACB=DFE∠(3)(3)若要以若要以““AASAAS””为依据,还缺条件____为依据,还缺条件______∠A=D∠(4)(4)若要以若要以““SSSSSS””为依据,还缺条件__为依据,还缺条件____AB=DEAC=DF(5)(5)若若∠∠B=DEF=90°∠B=DEF=90°∠要以要以““HL”HL”为依据,还缺为依据,还缺条件_____条件_____AC=DF证明三角形全等的思路:找两角夹边(ASA)找其它边(AAS)(1)已知两角对应相等(2)已知两边对应相等找第三边(SSS)找两边及夹角(SAS)任找一角(AAS、ASA)找角另一夹边(SAS)(3)已知一边一角对应相等证明题的分析思路:①要证什么②已有什么③还缺什么④创造条件缺什么④创造条件注意:1、结合图形审好题,必要时标记适当符号,并做到“由要证想需证,由已知想可知”。2、全等三角形,是证明两条线段相等或两个角相等的重要方法之一,证明时①要观察待证的线段或角,在哪两个可能全等的三角形中。②注意图中隐藏条件,如公共边、公共角、对顶角等,都可作为题中已知条件使用。====____AABBCCDDPP例例33已知:如图已知:如图,P,P是是BDBD上的任意一点上的任意一点AB=CB,AD=CD.AB=CB,AD=CD.求证求证:PA=PC:PA=PC①①要证要证明明PA=PCPA=PC,,需证需证ΔAPBΔCPB≌ΔAPBΔCPB≌或或ΔAPDΔCPD≌ΔAPDΔCPD≌(比如选择第一种情况)(比如选择第一种情况)②②已有两条边对应相等已有两条边对应相等(其中一条是公共边(其中一条是公共边BBPP))③③还缺一组夹角对应相等还缺一组夹角对应相等(缺∠(缺∠ABP=CBP∠ABP=CBP∠))④④创造条件(由创造条件(由已知已知想想可知可知))(由已知可证(由已知可证ΔABDΔCBD≌ΔABDΔCBD≌从而证从而证∠∠ABP=CBP∠ABP=CBP∠))分分析:析:====____AABBCCDDPP例例33已知:已知:PP是是BDBD上的任意一点上的任意一点AB=CB,AD=CD.AB=CB,AD=CD.求证求证PA=PCPA=PC证明:在△ABD和△CBD中AB=CBAD=CDBD=BD∴△ABDCBD(SSS)≌△∴∠ABD=CBD∠在△ABP和△CBP中AB=BC∠ABP=CBP∠BP=BP∴△ABPCBP(SAS)≌△∴PA=PC例4。已知:如图AB=AE,B=E∠∠,BC=EDAFCD⊥求证:点F是CD的中点分析:要证CF=DF可以考虑CF、DF所在的两个三角形全等,为此可添加辅助线构建三角形全等,如何添加辅助线呢?已有AB=AE,B=E∠∠,BC=ED怎样构建三角形能得到两个三角形全等呢?连结AC,AD添加辅助线是几何证明中很重要的一种思路证明:连结AC和AD∵在△ABC和△AED中,AB=AE,∠B=E∠,BC=ED∴△ABC≌△AED(SAS)∴AC=AD(全等三角形的对应边相等)∵AF⊥CD∴∠AFC=AFD=90°∠,在RtAFC△和RtAFD△中AC=AD(已证)AF=AF(公共边)∴RtAFC△≌RtAFD△(HL)∴CF=FD(全等三角形的对应边相等)∴点F是CD的中点小结:1、全等三角形的定义,性质,判定方法。2、证明三角形全等的思路。3、证明题的分析方法①要证什么②已有什么③还缺什么④创造条件缺什么④创造条件(由要证想需要证,由已知想可知)4、添加辅助线作业:1、课堂作业:课时达标P49-50(第3题,第6题的(2)小题不做)2、家庭作业:课时达标P50-52第6题、第9题的(2)小题、第10题、第12题不做;第11题、第19题选做。