正比例函数3VIP免费

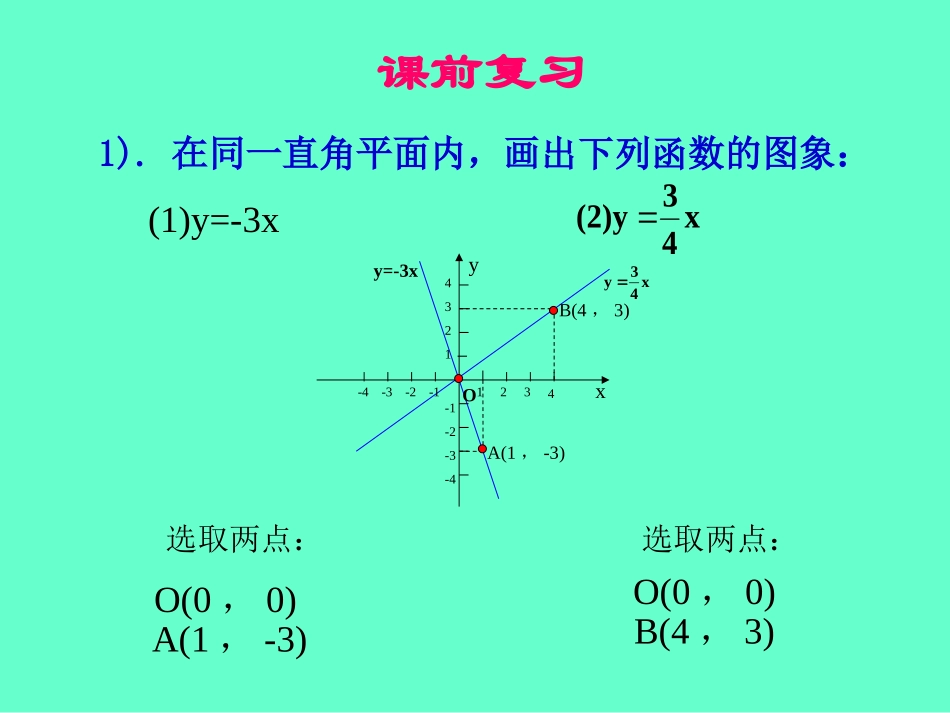
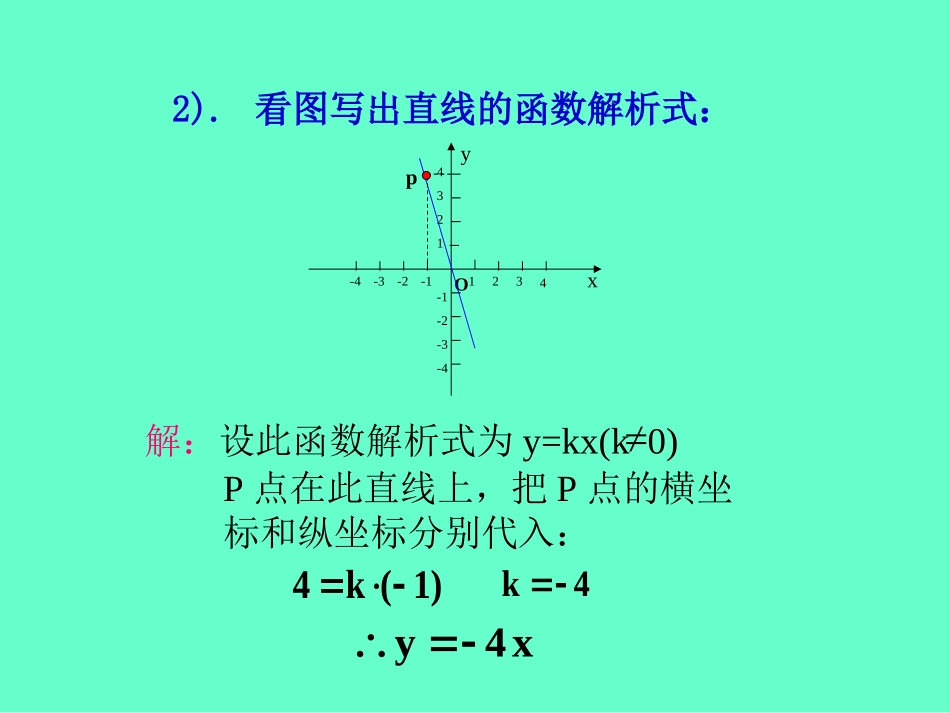
21.4正比例函数的图象与性质年级：八年级学科：数学制作：陈超课前复习1).在同一直角平面内，画出下列函数的图象：(1)y=-3x选取两点：O(0，0)A(1，-3)选取两点：O(0，0)B(4，3)x43(2)yy=-3xO1234-1-2-3-4-1-2-3-41234xyA(1，-3)B(4，3)x43y2).看图写出直线的函数解析式：解：设此函数解析式为y=kx(k0)P点在此直线上，把P点的横坐标和纵坐标分别代入：x4y1)(k44kO1234-1-2-3-4-1-2-3-41234xyp3).y-1与2x成正比例，且当x=-1时,y=5，求y与x的关系式。y=2kx+1把x=-1，y=5代入：5=-2k+1k=-2y=-4x+1解：x2k1y成正比例与x21y4).已知函数y=(m-2)xm2-3+m-n是正比例函数，求m，n的值。m2-3=1m-n=0m2=4，m=n解：02m2m2nm{该函数是正比例函数。2m注意：坐标轴上的点不属于任何象限！xy第一象限第二象限第三象限第四象限(+,+)(-,+)(-,-)(+,-)小练习指出下列各点所在象限或坐标轴：A(3，2)第一象限B(3，-2)第四象限C(-3，2)第二象限D(-3，-2)第三象限E(-3，0)x轴负半轴F(0，3)y轴正半轴(1)当k>0时，它的图象（除原点外）在第一、三象限内，自变量x逐渐增大时，y的值也随着逐渐增大。(2)当k<0时，它的图象（除原点外）在第二、四象限内，自变量x逐渐增大时，y的值则随着逐渐减小。0)的性质：kx(k正比例函数yO1234-1-2-3-4-1-2-3-41234xy3xyxyx31yO1234-1-2-3-4-1-2-3-41234xyx41yxy3xy课堂练习1).已知点A(m，n)在第二象限，则点B(-m，n+1)在第几象限？解：点A(m，n)在第二象限。m<0，n>0-m>0，n+1>0点B(-m，n+1)在第一象限。2).如果正比例函数y=(8-2a)x的图象经过二、四象限，求a的取值范围。比例系数k=8-2a<0a>4该函数图象经过二、四象限解：3).已知ab<0,则函数y=b/ax的图象经过第几象限？解：根据正比例函数的性质，k<0可得：该图象经过二、四象限。0ab异号。，ba0abk比例系数4).已知正比例函数y=(m+1)xm2+1，它的图象经过第几象限？解：该函数是正比例函数m2+1=1m2=0，m=0比例系数k=m+1把m=0代入k，k=1>0根据正比例函数的性质，k>0可得该图象经过一、三象限。01m1m{0m5).已知直线y=kx(k0)过点A(-2，4)，则点B(1，-2)是否在该直线上，为什么？分析：1.把点A的横坐标和纵坐标分别代入y=kx,解出k。2.求出该直线。3.把点B的横坐标和纵坐标代入该直线，若左右相等，则代表点B在该直线上。反之，则表示不在该线上。6).已知直线y=(a-2)x+a2-9经过原点，且y随x的增大而增大，求y与x的关系式.解：由题意得：把a=3代入y=(a-2)x02a3a09a23a{2a得关系式，y=x7).已知正比例函数过点A(-3,6)，B(t,1/4),求t的值。分析：1.求比例系数k。2.求出函数解析式。3.求t。已知点P(a,b)在第二象限内，直线y=-2x过点P，过点P作y轴的垂线，垂足为点A，若SPAO=4，求点p坐标。Δ讨论题xyxy2OAP小结正比例函数定义图象性质y=kx(k≠0)过原点的一条直线k>0k<0y的值随x的增大而减小y的值随x的增大而增大