正余弦函数的图像VIP免费

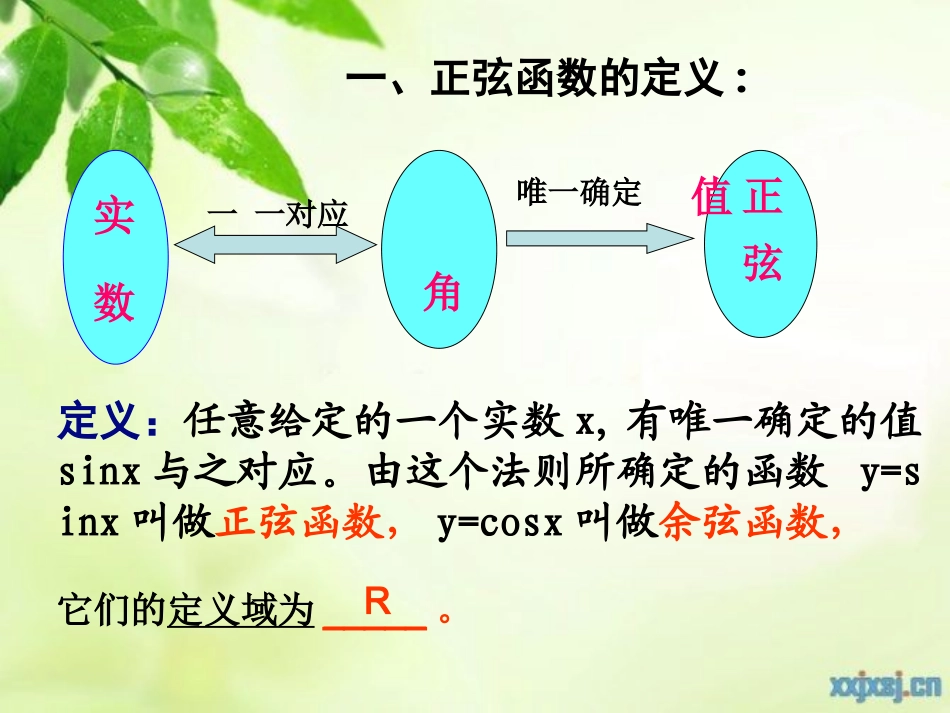
定义：任意给定的一个实数x,有唯一确定的值sinx与之对应。由这个法则所确定的函数y=sinx叫做正弦函数，y=cosx叫做余弦函数，实数正弦值角一一对应唯一确定一、正弦函数的定义:它们的定义域为_____。R遇到一个新的函数,先画出它的图象,然后通过观察图象获得对它性质的直观认识,是研究函数的基本方法.正弦函数、余弦函数的图象物理中把简谐运动的图像叫做“正弦曲线”或“余弦曲线”沙漏单摆实验探究1：如何画出正弦函数的图象？]2,0[,sinxxy1、描点法作图的三个步骤：______、_______、_______。2、取哪些点？作图准确吗？3、为了得到比较精确的正弦函数图象，如何从几何的角度用图形表示纵坐标？列表描点连线在直角坐标系中如何作点（，)?3sin3PMC(,)33sinyxO角的终边3想一想正弦线、余弦线的概念设任意角α的终边与单位圆交于点P.过点P做x轴的垂线,垂足为M.xyoα的终边P(x,y)M有向线段MP叫做角α的正弦线.有向线段OM叫做角α的余弦线.三角函数线从“形”的几何角度刻画了三角函数值的大小，利用单位圆中的正弦线作正弦函数的图象。y=sinx,x[0,2π]∈M1’P1’M2’P2’1-1xy0M1P1M2P21Oπ2π2321建立直角坐标系，在x轴上任取一点，作单位圆；1O1O5把角x的正弦线向右平移,使它的起点与x轴上的点x重合；6用光滑曲线把正弦线的终点连接起来,便得到y=sinx,x[0,2π]∈的图象.几何法作图2从圆与x轴的交点A起把圆分成12等分；1O1O4过圆上各分点作x轴的垂线，得到各对应角的正弦线；3把x轴上0到2这一段分成12等分;A利用正弦线画出的图象]2,0[,sinxxyyxo23423411y=sinxx[0,2]y=sinxxRsin(x+2k)=sinx,kZ正弦函数y=sinx,xR的图象叫正弦曲线.探究2：如何画出正弦函数的图象？sin,yxxR沿x轴左右平移x6yo--12345-2-3-41余弦函数的图象正弦函数的图象x6yo--12345-2-3-41余弦曲线正弦曲线形状完全一样只是位置不同左移个单位2y=cosxxRy=sinxxR=sin(x+)22------平移变换合作探究你能根据诱导公式，以正弦函数的图象为基础，通过适当的图形变换得到余弦函数的图象吗？yxo1-122322我们在作正弦函数y=sinx,x[0,2∈π]的图象时，描出了12个点，但其中起关键作用的点是哪些？分别说出它们的坐标。(0,0)(,1)2(,0)(,-1)23(2,0)五个关键点—(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)xsinx22302010-10最高点、最低点、与x轴的三个交点在精确度要求不高的情况下，我们常用“五点画图法”作出正弦函数和余弦函数的简图。与x轴的交点)0,0()0,()0,2(图象的最高点)1,(2图象的最低点)1(,23正弦曲线与x轴的交点)0,(2)0,(23图象的最高点)1,0()1,2(图象的最低点)1,(余弦曲线的五个关键点：xcosx2230210-101☞五点作图法的步骤①列表(列出对图象形状起关键作用的五点坐标)②描点(定出五个关键点)③连线(用光滑的曲线顺次连结五个点)“五点作图法”是我们画三角函数简图的基本方法。描点作图-2223211-xyo-xxsin1sinx101010210102232例1．画出下列函数的简图（1）y=sinx+1,x∈[0,2π]（2）y=－cosx,x∈[0,2π]列表解:（1）]2,0[,sin1xxy]2,0[,sinxxy2-22311xyo-(2)xxcosxcos0223210-101-1010-1]2,0[,cosxxy]2,0[,cosxxy典型例题五点法作图(2)描点(1)列表(3)连线思考：能否从图象变换的角度出发得到（1）（2）的图象？列表(2)描点连线解:（1）Y2X02y=2sinx1y=sinx1.用五点法画出y=2sinx,x∈[0，]的简图22.用图象变换法画出y=sin(-x),x∈[0，]的简图;223变式训练2.用图象变换法画出y=sin(-x),x∈[0，]的简图;223由诱导公式知3sincos2xx1-12xyo232223...