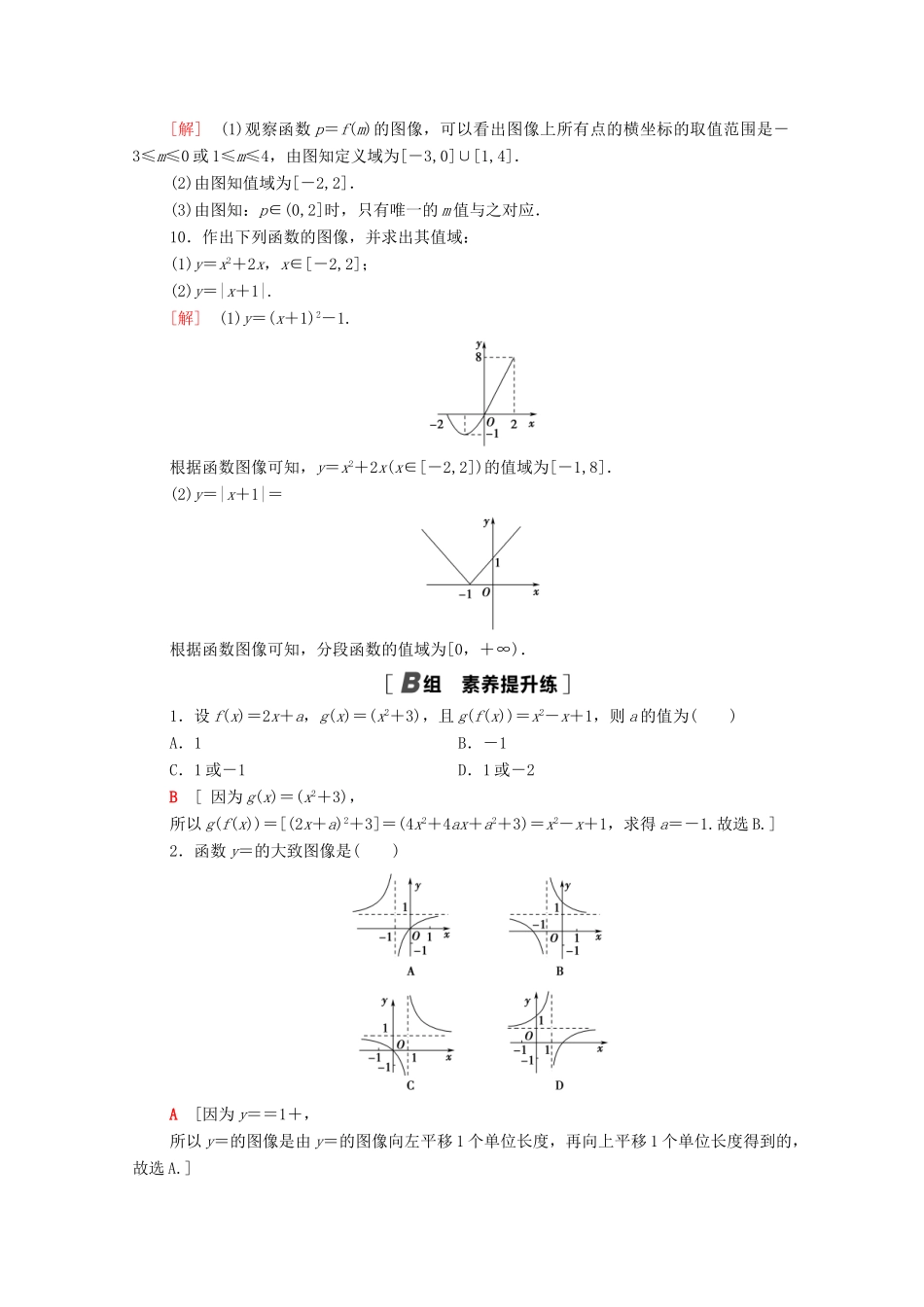
课时分层作业(六)函数的表示法(建议用时:60分钟)一、选择题1.已知函数f(x)的图像如图所示,则此函数的定义域、值域分别是()A.(-3,3),(-2,2)B.[-3,3],[-2,2]C.[-2,2],[-3,3]D.(-2,2),(-3,3)B[由图可知自变量-3≤x≤3,函数值-2≤y≤2.故定义域为[-3,3],值域为[-2,2].]2.设f(x)=则f(5)的值为()A.8B.9C.10D.11A[由题意易知,f(5)=f[f(11)]=f(8)=f[f(14)]=f(11)=8.故选A.]3.函数y=x+的图像是()C[y=x+=如图:]4.设g(x)=2x+3,g(x+2)=f(x),则f(x)等于()A.-2x+1B.2x-1C.2x-3D.2x+7D[由g(x)=2x+3,知f(x)=g(x+2)=2(x+2)+3=2x+7.]5.若x∈R,f(x)是y=2-x2,y=x这两个函数的较小者,则f(x)的最大值为()A.2B.1C.-1D.无最大值B[在同一坐标系中画出函数y=2-x2,y=x的图像如图所示,根据题意,坐标系中实线部分即为函数f(x)的图像.∴当x=1时,f(x)max=1.]二、填空题6.如图,函数f(x)的图像是折线段ABC,其中点A,B,C的坐标分别为(0,4),(2,0),(6,4),则f{f[f(2)]}=________.2[由题意可知f(2)=0,f(0)=4,f(4)=2.因此,有f{f[f(2)]}=f[f(0)]=f(4)=2.]7.如果f=,则当x≠0且x≠1时,f(x)=________.[法一:因为x≠0且x≠1,所以f=,即f(x)=.法二:令=t,因为x≠0且x≠1,所以t≠0且t≠1,x=,则f(t)==,即f(x)=.]8.某城市出租车按如下方法收费:起步价6元,可行3km(含3km),3km后到10km(含10km)每多走1km(不足1km按1km计)加价0.5元,10km后每多走1km加价0.8元,某人坐出租车走了13km,他应交费________元.11.9[由题意,设出租车行驶了xkm,应交费f(x)元,则f(x)=所以当x=13时,f(x)=6+0.5(10-3)+0.8(13-10)=11.9.]三、解答题9.已知函数p=f(m)的图像如图所示.求:(1)函数p=f(m)的定义域;(2)函数p=f(m)的值域;(3)p取何值时,只有唯一的m值与之对应.[解](1)观察函数p=f(m)的图像,可以看出图像上所有点的横坐标的取值范围是-3≤m≤0或1≤m≤4,由图知定义域为[-3,0]∪[1,4].(2)由图知值域为[-2,2].(3)由图知:p∈(0,2]时,只有唯一的m值与之对应.10.作出下列函数的图像,并求出其值域:(1)y=x2+2x,x∈[-2,2];(2)y=|x+1|.[解](1)y=(x+1)2-1.根据函数图像可知,y=x2+2x(x∈[-2,2])的值域为[-1,8].(2)y=|x+1|=根据函数图像可知,分段函数的值域为[0,+∞).1.设f(x)=2x+a,g(x)=(x2+3),且g(f(x))=x2-x+1,则a的值为()A.1B.-1C.1或-1D.1或-2B[因为g(x)=(x2+3),所以g(f(x))=[(2x+a)2+3]=(4x2+4ax+a2+3)=x2-x+1,求得a=-1.故选B.]2.函数y=的大致图像是()A[因为y==1+,所以y=的图像是由y=的图像向左平移1个单位长度,再向上平移1个单位长度得到的,故选A.]3.若函数f(x)满足f=x2+,则f()=________.3[∵f=x2+=-2,∴f(x)=x2-2,∴f()=()2-2=3.]4.已知函数f(x)=若f[f(x0)]=2,则x0的值为________.-2或4[法一:由已知得,f(x)=|x-1|,又f[f(x0)]=2,则||x0-1|-1|=2,解得x0=-2或4.法二:依题意,或所以f(x0)=3或-1.当f(x0)=3时,或解得x0=-2或4.当f(x0)=-1时,或x0不存在.综上得x0=-2或4.]5.如图所示,在边长为4的正方形ABCD边上有一点P,由点B(起点)沿着折线BCDA,向点A(终点)运动.设点P运动的路程为x,△APB的面积为y,求y与x之间的函数解析式.[解]当0≤x≤4时,S△APB=×4x=2x;当4