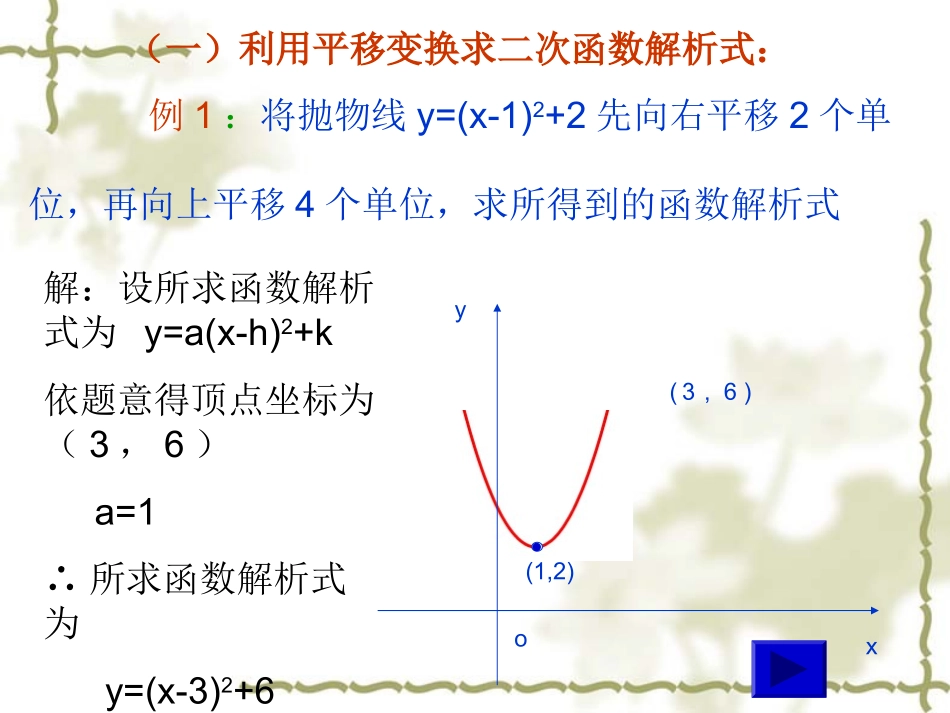
例1:将抛物线y=(x-1)2+2先向右平移2个单位,再向上平移4个单位,求所得到的函数解析式yxo(1,2)(,)36解:设所求函数解析式为y=a(x-h)2+k依题意得顶点坐标为(3,6)a=1∴所求函数解析式为y=(x-3)2+6(一)利用平移变换求二次函数解析式:规律:自变量:左加右减常量:上加下减变式训练:将抛物线y=2x2沿着直线y=x平移个单位后,其顶点在直线上的A点处,求平移后的函数解析式.2Ay=xxoy2?y=2x2(,)例2:若抛物线C1:y=(x-1)2+2与抛物线C2关于y轴对称,求抛物线C2的函数解析式。y=(x-1)2+2yxo(1,2)(,)将抛物线y=(x-1)2+2先向右平移2个单位,再向上平移4个单位,求所得到的函数解析式(二)利用对称规律求二次函数解析式-12?解:设所求抛物线解析式为y=a(x-h)2+k依题意得顶点坐标为(-1,2)a=1∴所求抛物型解析式为y=(x+1)2+2变式训练:(1)若抛物线C1:y=(x-1)2+2与抛物线C2关于x轴对称,求抛物线C2的函数解析式yox(,)(,)yxo(2)若抛物线C1:y=(x-1)2+2与抛物线C2关于原点对称,求抛物线C2的函数解析式。(1,2)(,)-1-2例3:将抛物线y=(x-1)2+2绕着它的顶点旋转180°后,求所得到的函数解析式yxoy=(x-1)2+2(三)运用旋转规律求二次函数解析式解:设所求抛物线的解析式为y=a(x-h)2+k依题意得顶点坐标为(1,2)开口方向已改变,则a=-1∴所求抛物线的解析式为y=-(x-1)2+2yxo变式训练:(1)将抛物线y=(x-1)2+2绕着坐标原点旋转180°后,求所得到的函数解析式y=(x-1)2+2(1,2)(,)(2)将抛物线y=(x-1)2+2绕着它与y轴的交点H旋转180°后,求所得到的函数解析式yxoy=(x-1)2+2(1,2)(,)利用图形变换规律求二次函数解析式:1.这节课我们学习了什么内容?2.利用变换规律确定二次函数解析式时,关键是确定抛物线的什么东西?3.通过这节课学习,你知道了哪些规律?练习、作业:3.将抛物线y=(x-1)2+2沿着直线y=x向右上角方向平移个单位后,求平移后的函数解析式.22.将抛物线y=(x-1)2+2绕着A(-2,3)旋转180后,求所得到的函数解析式1.若抛物线C1:y=(x-1)2+2与抛物线C2关于直线x=-2对称,求抛物线C2的函数解析式