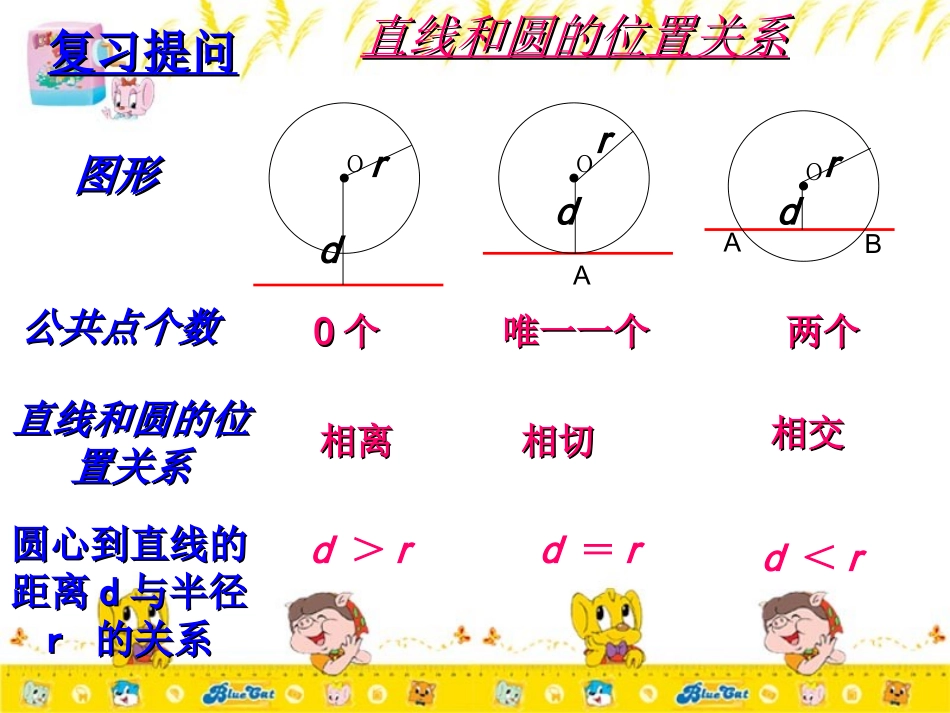
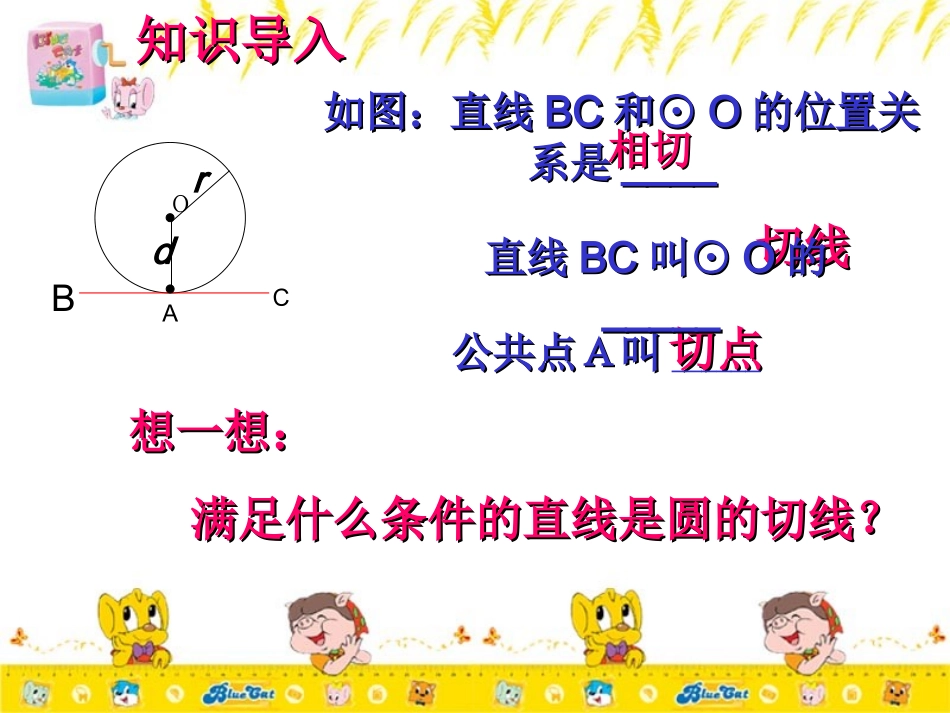
3.2.2圆的切线的判定直线和圆的位置关系直线和圆的位置关系图形图形公共点个数公共点个数直线和圆的位直线和圆的位置关系置关系圆心到直线的圆心到直线的距离距离dd与半径与半径rr的关系的关系00个个唯一一个唯一一个两个两个相离相离相切相切相交相交d<rd=rd>rOOOdrdrdrAAB复习提问复习提问OdrBCA知识导入知识导入如图:直线如图:直线BCBC和⊙和⊙OO的位置关的位置关系是系是________切线切线切点切点公共点A叫公共点A叫______想一想:想一想:满足什么条件的直线是圆的切线?满足什么条件的直线是圆的切线?直线直线BCBC叫⊙叫⊙OO的的__________相切相切知识导入知识导入OABC经过半径的外端半径的外端并且垂直于这条半径垂直于这条半径的直线是圆的切线。切线的判定定理:OAOA为为⊙O半径BCBC⊥OA于ABCBC为为⊙O切线温馨提示:温馨提示:在此定理中,题设是“经过半径的外端”和“垂直于这条半径”,两个条件缺一不可,否则就不是圆的切线,1、直线l垂直于半径OA,直线l是⊙O的切线吗?2、直线l经过半径OA的外端A,直线l是⊙O的切线吗?不是不是不是不是切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线切线的判定方法有几种,分别是什么?1、直线与圆有唯一公共点2、圆心到直线的距离等于该圆的半径3、切线的判定定理:经过半径的外端,并且垂直垂直于这条半径的直线是圆的切线。例1、如图,已知直线AB经过⊙O上的点A,且AB=OA,∠OBA=45°,直线AB是⊙O的切线吗?为什么?ooAABB分析:要证明一条直线是圆的切线,必须符合两个条件,其一是这条直线是否经过半径外端,其二是这条直线是否与这条半径垂直,若满足这两个条件,就能说明这条直线是圆的切线。解:直线AB是⊙O的切线.理由如下:因为AB=OA,且∠OBA=45°,所以∠AOB=45°,∠OAB=90∴ABOA⊥,又OA是⊙O的半径,所以直线AB是⊙O的切线例2:已知直线AB经过⊙O上的点C,并且OA=OB,CA=CB,求证:直线AB是⊙O的切线。·OACB证明:连结OC,则因:OA=OBAC=BC得:OC是等腰△ABC底边上的中线∴ABOC⊥,又OC是⊙O的半径,∴AB是⊙O的切线。练习一:判断题1、和圆有一个公共点的直线是圆的切线2、和半径垂直的直线是圆的切线3、经过半径的外端的直线是圆的切线练习二:已知:AD是∠BAC的平分线,设O为AD上的任一点,并且OE⊥AB于点E.求证:以O为圆心,以OE为半径的圆⊙O与AB、AC相切BDCAOE(2012.山东淄博)已知:AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,∠CAB=30°。求证:DC是⊙O的切线OCABD