1.1.6棱柱、棱锥、棱台和球的表面积VIP免费

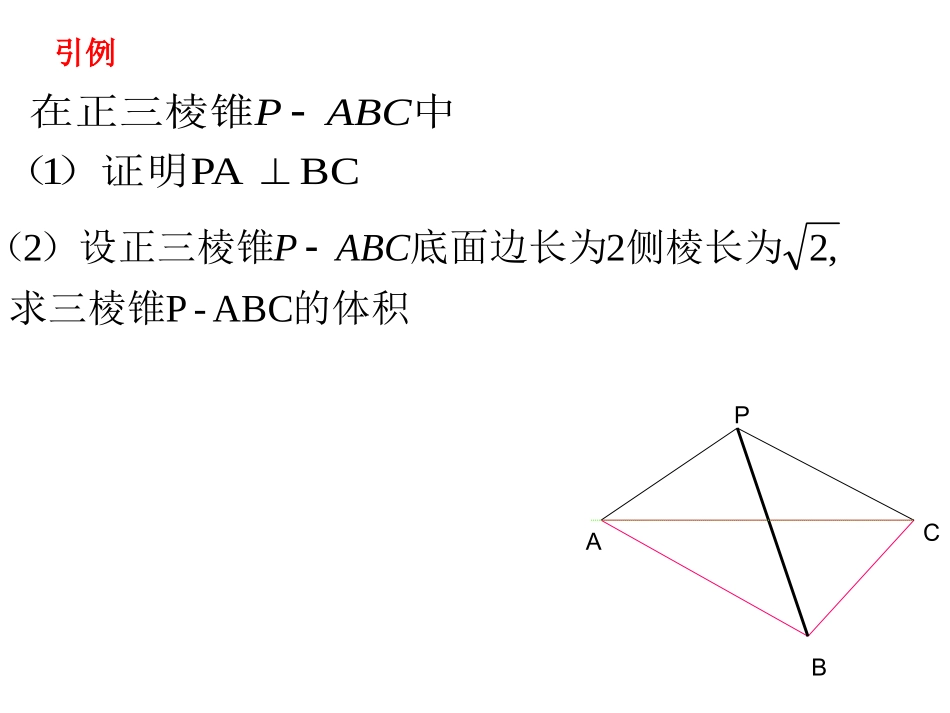
CPABBCPA1）证明（中在正三棱锥ABCP的体积求三棱锥侧棱长为底面边长为）设正三棱锥（ABC-P,222ABCP引例BCPA1）证明（中在正三棱锥ABCP引例PABCPAHPAPAHBCPAHAHPHHAHPHBCPHBCAHBCHABC-PPHAHHBC面又面面，又；中点，为且有正三棱锥，，，连结中点证明：取CPABHCPAB的体积求三棱锥，侧棱长为底面边长为）设正三棱锥（ABC-P,222ABCPO引例36PO3322PAPAOROABC-PAOOP2，，中，在为底面中心，，正三棱锥，，连结在底面的射影为）解：做（AOt3236331S31VABC-Ph几何体体积的求法CPABBCPA1）证明（中在正三棱锥ABCP36PO3322PAPAOROABC-PAOOP2，，中，在为底面中心，，正三棱锥，，连结在底面的射影为）解：做（AOt3236331S31VABC-Ph的体积求三棱锥，侧棱长为底面边长为）设正三棱锥（ABC-P,222ABCPO引例一、直接法所给的是规范几何体,且已知条件比较集中时,就按所给几何体的方位用公式直接计算体积.CPAB引例思考：除了“直接法”还有其他求该几何体体积的方法吗？的体积求三棱锥，侧棱长为底面边长为）设正三棱锥（ABC-P,222ABCP换补割PABC.,PAPBC三棱锥的高为则为底面选平面换：PABC.PCPB,,:,422A,222222PBCPAPCPAPBPAPBPAABBPAB面，故同理即中在.,PAPBC三棱锥的高为则为底面选平面.32PAPCPB2131A31PSVPBC换：返回将正三棱锥补成一个棱长为的正方体2补：CBAP3222261V61V正方体三棱锥容易推得补：将三棱锥补成一个棱长为的正方体2返回CPABH正三棱锥被截面PAH所截，分割成两个三棱锥，由（1）证明可知，BC面PAH32BCS31PAHV割：二、换底法一、直接法所给的是规范几何体,且已知条件比较集中时,就按所给几何体的方位用公式直接计算体积.当按所给几何体的方位不便计算时,可选择条件较集中的面作底面,以便计算底面积和高.所给的是非规范(或条件比较分散的规范的)几何体时,通过对几何体的割补或体积变换,化为与已知条件直接联系的规范几何体,并作体积的加、减法。三、割补法练1.已知正方体ABCD—A1B1C1D1的棱长为2,求三棱锥B1—AD1C的体积。ABCDA1B1C1D138V31V正方体三棱锥练习1变式，四面体S-ABC的三组对棱分别相等，且依次为，求该四体的体积。分析：由三条对棱相等，易联想到长方体的三组相对的面上的对角线相等，因此可将四面体补成一个长方体来解。25135，，222222222(25)4(13)2354146183DSABxyxyzyzxzVVVVVV－四面体长方体长方体长方体长方体解：设长方体的三边长分别为x,y,z.则解得：＝－＝－＝SBDC练习2：在边长为a的正方体ABCD—A1B1C1D1中，M、N、P分别是棱A1B1、A1D1、A1A上的点，且满足A1M=21A1B1，A1N=2ND1，A1P=43A1A，如图，试求三棱锥A1—MNP的体积．MNAPMNPAVV11解：.241433221213121313111aaaaPANAMA练习2：在边长为a的正方体ABCD—A1B1C1D1中，M、N、P分别是棱A1B1、A1D1、A1A上的点，且满足A1M=21A1B1，A1N=2ND1，A1P=43A1A，如图，试求三棱锥A1—MNP的体积．求体积的常用方法所给的是非规范(或条件比较分散的规范的)几何体时,通过对几何体的割补或体积变换,化为与已知条件直接联系的规范几何体,并作体积的加、减法。小结当按所给几何体的方位不便计算时,可选择条件较集中的面作底面,以便计算底面积和高.所给的是规范几何体,且已知条件比较集中时,就按所给几何体的方位用公式直接计算体积.换底法直接法割补法思考题：.如图，在多面体ABCDEF中，已知面ABCD是边长为3的正方形，EF//AB，EF垂直AE，EF=3/2，EF与面AC的距离为2，求该多面体的体积()。ABCDEF915..5.6.22ABCD思考题：.如图，在多面体ABCDEF中，已知面ABCD是边长为3的正方形，EF//AB，EF垂直AE，EF=3/2，EF与面AC的距离为2，求该多面体的体积()。ABCDEF915..5.6.22ABCD法一：分别取AB、CD的中点G、H连EG，GH，EH，把该多面体分割成一个四棱锥与一个三棱柱，可求得四棱锥的体积为3，三棱柱的体积，整个多面体的体积为．故选D．15292ABCDEFGH法二.由已知条件可知...