2.3一元二次方程根的判别式VIP免费

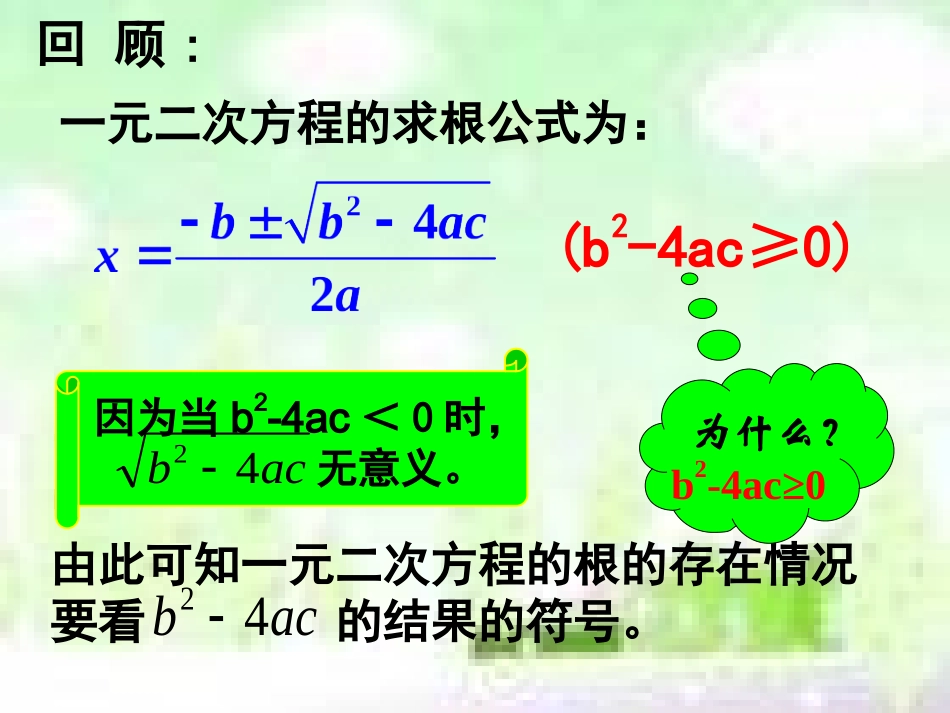
acb42桃源县文昌中学罗惠英湘教版数学九年级上册2.会根据一元二次方程根的情况，灵活运用一元二次方程根的判别式构建不等式(组)，从而确定方程中待定系数的取值范围。1.会运用根的判别式判定一元二次方程根的情况。一元二次方程根的判别式灵活运用一元二次方程根的判别式，确定方程中待定系数的取值范围。一元二次方程的求根公式为：回顾:由此可知一元二次方程的根的存在情况要看的结果的符号。acb42(b2-4ac≥0)为什么？b2-4ac≥0因为当b2-4ac＜0时，无意义。acb42一元二次方程根的判别式acb42把b2-4ac叫做一元二次方程ax2+bx+c=0(a≠0)的根的判别式记作“”，即1.当时,方程有两个不相等的实数根2.当时,方程有两个相等的实数根3.当时,方程没有实数根240bac240bac240bac若△≥0时,方程有两个实数根一元二次方程根的判别情况（1）04322xx（3）07152xx（2）yy249162解:(1) △=b2-4ac例：不解方程，判断下列方程根的情况：∴原方程有两个不相等的实数根。=32－4×2×(-4)=41＞0(2)原方程化一般式为：16y2－24y＋9=0 △=b2-4ac=(-24)2－4×16×9=0∴原方程有两个相等的实数根。方程一定要先化为一般式(3)原方程化一般式为：5x2－7x＋5=0 △=b2-4ac=(-7)2－4×5×5=-51＜0∴原方程没有实数根。一.化二.算三.判四.结不解方程，判断下列方程根的情况：(1)x2－2x＋3=0(2)2x(x－3)=－3(3)x2＋9=6x解： △=b2-4ac=(-2)2－4×1×3=-8＜0∴原方程没有实数根。解：原方程化一般式为2x2－6x＋3=0 △=b2-4ac∴原方程有两个不相等的实数根。=(-6)2－4×2×3=12＞0解：原方程化一般式为：x2－6x＋9=0 △=b2-4ac=(-6)2－4×1×9=0∴原方程有两个相等的实数根。化一般式化一般式在一元二次方程中若a与c异号，则方程中)0(02acbxax()A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.根的情况无法acb42△acb420ac＜0A1.当时,方程有两个不相等的实数根2.当时,方程有两个相等的实数根3.当时,方程没有实数根如何用根的判别式“△=b²-4ac”判断一元二次方程根的情况？反之，成立吗？△=b²－4ac＞0△=b²－4ac=0△=b²－4ac＜0反之，当知道一元二次方程根的情况时，也可得到关于“△”的不等式，从而可以确定方程中待定系数的取值范围。一元二次方程的根的情况：反过来：1.当方程有两个不相等的实数根时，2.当方程有两个相等的实数根时，3.当方程没有实数根时，240bac240bac240bac若方程有(两个)实数根则△≥0注意运用△时,必须把所给的方程化成一般形式后方可使用。a≠0是使用根的判别式的前提条件0mx)1m2(mx2若关于x的一元二次方程：有两个实数根，求m的取值范围.mcmbma),12(,解：14=m4)]12(22-=[-mm42=acb 方程有两个实数根∴≥a≠0即m≠04m+1≥041m∴m的取值范围是且m≠0．注意：a≠0是使用根的判别式的前提条件已知方程及其根的情况，求字母的取值范围。=4m²+4m+1-4m²当k取什么值时，关于x的方程：(1)方程有两个不相等的实根；(2)方程有两个相等的实根；(3)方程无实根；01214222kxkx解:89k89k89k已知方程及其根的情况，求字母的取值范围。△=[-(4k+1)]2-4×2(2k²-1)=16k²+8k+1-16k²+8=8k+9(1) 方程有两个不相等的实数根∴△=8k+9＞0∴(2) 方程有两个相等的实数根∴△=8k+9=0∴(3) 方程无实数根∴△=8k+9＜0∴求证：关于x的方程：有两个不相等的实根。01222mxmx∴原方程有两个不相等的实数根。 △=[-(m+2)]²-4(2m-1)=m²+4m+4-8m+4=m²-4m+8=m²-4m+4+4=(m-2)²+4而对于任意实数m都有(m-2)²≥0证明：∴(m-2)²+4＞0即△＞0一元二次方程有两个实数根,则m的取值范围是______________02212mmxxm21422mmm解844422mmm84m02m101mm即又12mm且变达标测试一、选择题：1、已知关于X的一元二次方程kx2-2x+1=0有实数根，则k的取值范围是（）Ａ）k<１Ｂ）k≤１Ｃ）k<１且k≠0Ｄ）k≤１且k≠02、若关于y的方程ay２-4y...