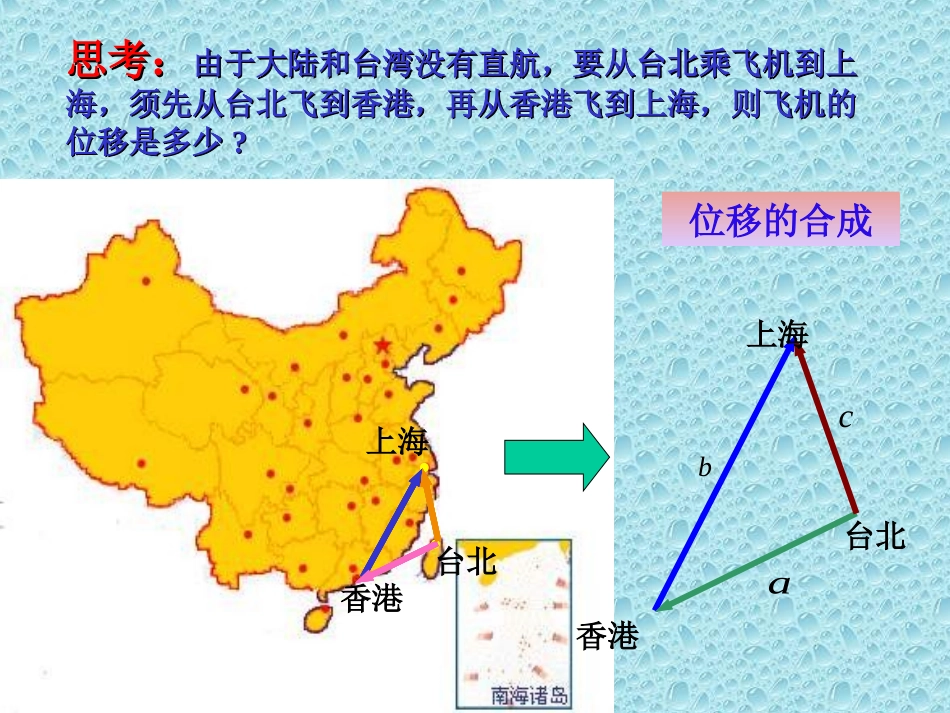
零向量、单位向量概念:向量的概念:向量的表示方法:共线向量与平行向量关系:平行向量定义:相等向量定义:位移的合成台北香港上海思考:思考:由于大陆和台湾没有直航,要从台北乘飞机到上由于大陆和台湾没有直航,要从台北乘飞机到上海,须先从台北飞到香港,再从香港飞到上海,则飞机的海,须先从台北飞到香港,再从香港飞到上海,则飞机的位移是多少位移是多少??abc上海台北香港探究图2.2-2表示橡皮条在两个力的作用下,沿着GC的方向伸长了EO;图2.2-3表示撤去F1和F2,用一个力F作用在橡皮条上,使橡皮条沿着相同的方向伸长相同的长度。力F对橡皮条产生的效果,与力F1与F2共同产生的效果相同,物理学中把力F叫做F1与F2的合力.由图2.2-4发现,力F在以力F1、F2为邻边的平行四边形的对角线上,并且大小等于平行四边形的对角线的长。力的合成图2.2-41.向量加法的三角形法则:abbaabCAB,,,,abAABaBCbACabababABBCAC�����、内点,则与,记则这称为已知非零向量在平面任取一作向量叫做的和作即种求向量和向量加法的三角方法,形法的。首尾顺次相连起→终位移的合成可以看作向量加法三角形法则的物理模型。位移的合成可以看作向量加法三角形法则的物理模型。还有没有其他的做法?abo·ABC力的合成可以看作向量加法的平行四边形法则的物理模型。力的合成可以看作向量加法的平行四边形法则的物理模型。作法(1)在平面内任取一点OOB==�(2)作OAa,b=+�(3)OCab作同起点的对角线BOCAab以同一点O为起点的两个已知向量为邻边作OACB,则以O为起点的对角线OC就是的和.ba、ba与例1如图2.2-7,已知向量a、b,求作向量a+b.ab图2.2-7oABCACab=+�ACab=+�(1)向同(2)反向abab当向量是共线向量时又如何作出来?a,b,a+bABCABCa+=+=a00a规定:请同学们快速完成84页练习1、2题P84课堂练习判断的大小||||||abab++与1、不共线abo·ABb+ab�a||||||abab++