2.2.1一次函数的性质与图象VIP免费

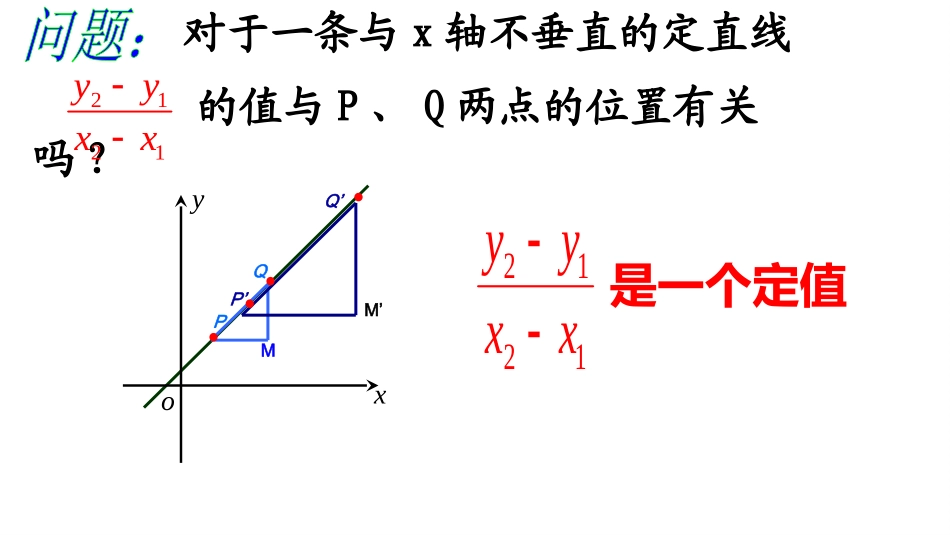
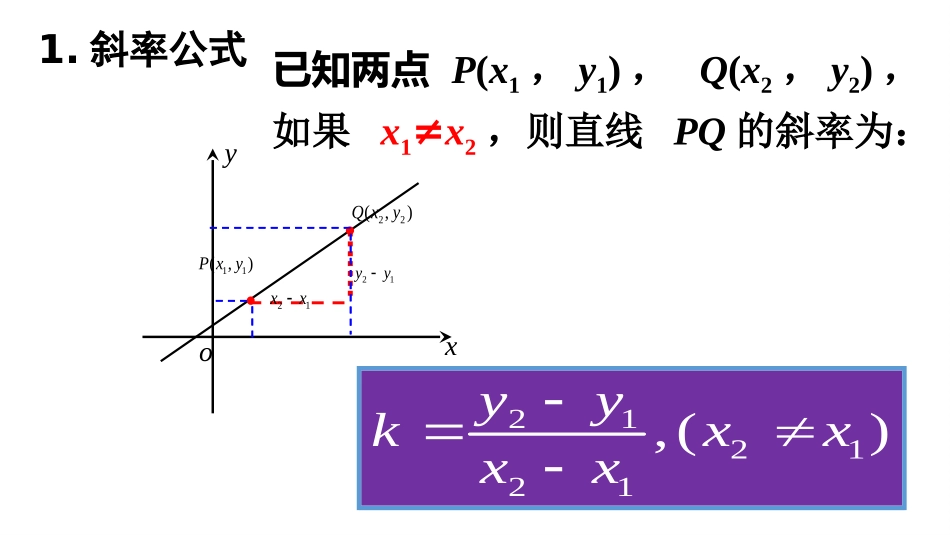
直线的斜率本溪市高级中学宫瑞阳xyo是一个定值对于一条与x轴不垂直的定直线的值与P、Q两点的位置有关吗?2121yyxx2121yyxxPQP’Q’MM’已知两点P(x1，y1)，Q(x2，y2)，如果x1≠x2，则直线PQ的斜率为：xyo11(,)Pxy22(,)Qxy21xx21yy1.斜率公式212121,()yykxxxxxyo),(111yxP),(222yxP1y2y1212xxyyk如果x1=x2，斜率不存在，因为分母为0。当直线与坐标轴平行或重合时,直线的斜率如何？oyxl222(,)Pxy111(,)Pxy21210yykxx如果y1=y2，斜率为0。通常，我们把直线中的系数叫做这条直线的斜率.垂直于轴的直线，斜率不存在.2.直线斜率的定义3.斜率公式的形式特点：(1)与两点的顺序无关;(2)公式表明,直线的斜率可以通过直线上任意两(3)当x1=x2时,直线不存在斜率.点的坐标来表示；111222(,),(,)PxyPxy经过两点的直线的斜率公式212121,()yykxxxxk斜率刻画了什么？xyAOB1x1y2x2yxy1122(,),(,)AxyBxy212121,()yykxxxx令：2121,xxxyyy,(0)ykxx斜率刻画了直线的倾斜程度xyo1l2l3l的大小关系为则的斜率分别为设直线如图321321321,,,,,,,,kkkkkklll213kkk练习：4.直线的倾斜角直线的方向除了利用直线的斜率以外，还可以利用角度来刻画。x轴正向与直线向上的方向所成的角叫做这条直线的倾斜角（用α或θ表示）。规定：若直线与x轴平行或重合，则其倾斜角为零度角。αααxyBAO11直线向上的方向与x轴正方向所成的角倾斜角下列四图中，表示直线的倾斜角的是()试一试ayxoAyxoaBayxoCyxaoDApoyxlypoxlpoyxlpoyxl直线的倾斜角范围直线倾斜角α的范围为：议一议：如果一条直线绕着一点旋转，则它的倾斜角有什么变化？0°≤α＜180°poyxlypoxlpoyxlpoyxl0°＜＜90°=90°90°＜<180°=0°k=0k>0斜率不存在k<0斜率和倾斜角的关系归纳：斜率k与倾斜角之间的关系越大，倾斜角越大。此时，时，倾斜角为锐角，KK0越大，倾斜角也越大。此时，时，倾斜角为钝角，KK0例题1.直线过点A(-2,0),B(-5,3),求直线AB的斜率。解：𝑘=𝛥𝑦𝛥𝑥=3−3=−1𝑥1=−2,𝑥2=−5,𝑦1=0,𝑦2=3𝛥𝑥=−5−(−2)=−3,𝛥𝑦=3−0=3例题2.画出方程3x+6y-8=0的图像。解：由已知方程解出y，得：𝑦=−12𝑥+43这是一次函数的表达式，它的图像是一条直线.当𝑥=0时，𝑦=43；当𝑥=2时，𝑦=13.做直线AB，即为所求方程的图像.练习1.把满足下列条件的直线的方程写成一次函数的形式（提示：用待定系数法）（1）斜率k=5，且过点（0，-3）；（2）斜率k=-3，且过点（3，-1）.练习2.已知两点,直线过点且与线段相交，试求的斜率取值范围.解：过点P且与MN相交的直线，必在PM和PN之间.因为𝑘𝑃𝑁=¿¿且在过点P且与MN相交的直线中，不含垂直于𝑥轴的直线.所以直线l的斜率的取值范围为56≤𝑘≤6.练习3.已知两点，过点的直线与线段有公共点.求直线斜率的取值范围；解：如图，由题意可知𝑘𝑃𝐴=4−0−3−1=−1,𝑘𝑃𝐵=2−03−1=1.要使直线l与线段AB有公共点，则直线l的斜率k的取值范围是𝑘≤−1.或思考探索.已知函数的图象的一段圆弧（如图所示）则（）C课堂小结1.直线斜率的定义2.斜率的公式3.倾斜角的定义4.倾斜角的取值范围5.倾斜角和斜率的联系