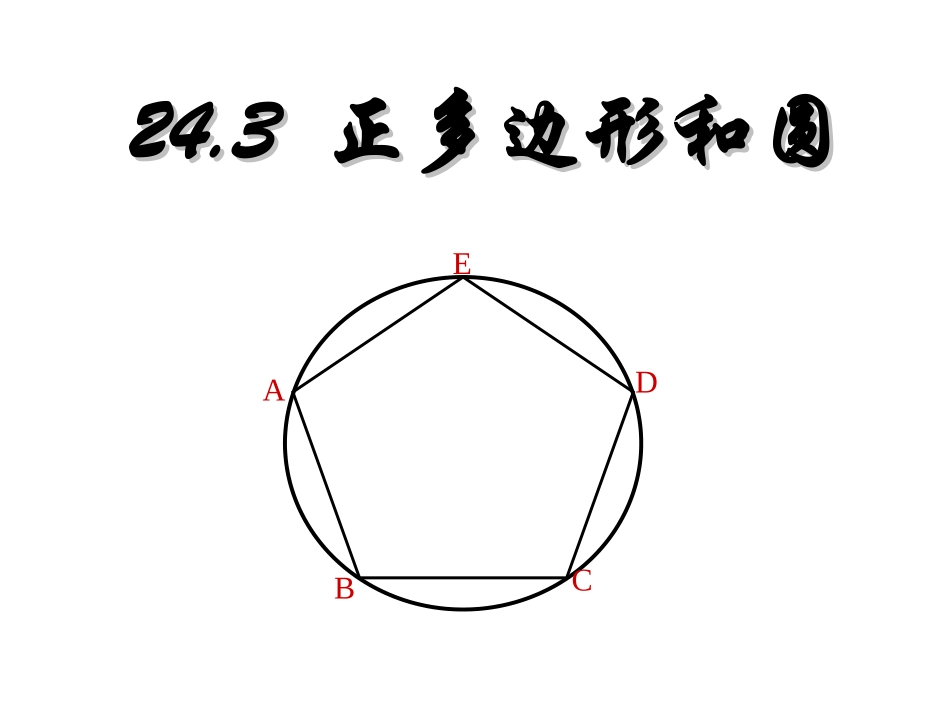
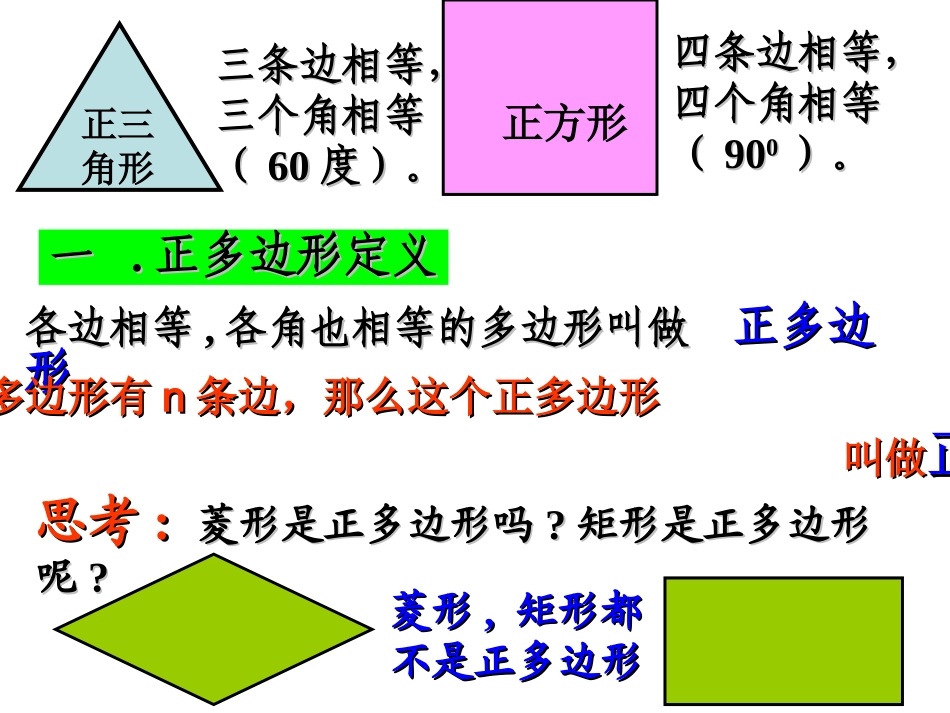
24.324.3正多边形和圆正多边形和圆ABCDE观察下列图形他们有什么共同特点?各边相等各边相等,,各角也相等的多边形叫做各角也相等的多边形叫做正多边正多边形形..三条边相等,三条边相等,三个角相等三个角相等((6060度)。度)。四条边相等,四条边相等,四个角相等四个角相等((909000)。)。正三角形正方形一一..正多边形定义正多边形定义如果一个正多边形有如果一个正多边形有nn条边,那么这个正多边形条边,那么这个正多边形叫做叫做正正nn边形边形。。思考思考::菱形是正多边形吗菱形是正多边形吗??矩形是正多边形矩形是正多边形呢呢??菱形菱形,,矩形都矩形都不是正多边形不是正多边形正n边形与圆的关系1.把正n边形的边数无限增多,就接近于圆.2.怎样由圆得到多边形呢?ABCD思考1:把一个圆4等分,并依次连接这些点,得到正多边形吗?弧相等弧相等弦相等(多边形的边相等)弦相等(多边形的边相等)圆周角相等(多边形的角相等)圆周角相等(多边形的角相等)—多边形是正多边形多边形是正多边形思考2:把一个圆5等分,并依次连接这些点,得到正多边形吗?证明:证明: AB=BC=CD=DE=EAB=BC=CD=DE=EAAABCDE⌒⌒⌒⌒⌒∴∴AB=BC=CD=DE=EAAB=BC=CD=DE=EA BCE=CDA=3ABBCE=CDA=3AB⌒∴∠∴∠A=B∠A=B∠同理∠同理∠B=C=D=E∠∠∠B=C=D=E∠∠∠∴∠∴∠A=B=C=D=E∠∠∠∠A=B=C=D=E∠∠∠∠又 顶点又 顶点AA、、BB、、CC、、DD、、EE都在⊙都在⊙OO上上∴∴五边形五边形ABCDEABCDE是⊙是⊙OO的的内接正五边内接正五边形形..定理1:把圆分成n(n≥3)等份:依次连结各分点所得的多边形是这个圆的内接正多边形.又 五边形PQRST的各边都与⊙O相切,∴五边形PQRST的是O外切正五边形。证明:连结OA、OB、OC,则:∠OAB=OBA=OBC=OCB∠∠∠ TP、PQ、QR分别是以A、B、C为切点的⊙O的切线∴∠OAP=OBP=OBQ=OCQ∠∠∠∴∠PAB=PBA=QBC=QCB∠∠∠又 AB=BC∴AB=BC∴△PAB与△QBC是全等的等腰三角形。∴∠P=QPQ=2PA∠同理∠Q=R=S=T∠∠∠QR=RS=ST=TP=2PA⌒⌒ABCDEPQRSTO定理2:经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正多边形.思考3:过圆的5等分点画圆的切线,则以相邻切线的交点为顶点的多边形是正多边形吗?EFCD..OO中心角半径半径RR边心距r正多边形的中心正多边形的中心::一个正多边形的一个正多边形的外接圆的圆心外接圆的圆心..正多边形的半径正多边形的半径::外接圆的半径外接圆的半径正多边形的中心角正多边形的中心角::正多边形的每一条正多边形的每一条边所对的圆心角边所对的圆心角..正多边形的边心距:正多边形的边心距:中心到正多边形的中心到正多边形的一边的距离一边的距离..二二..正多边形有关的概正多边形有关的概念念1.O是正△ABC的中心,它是△ABC的_____圆与________圆的圆心。2.OB叫正△ABC的_____,它是正△ABC的______圆的半径。3.OD叫作正△ABC______,它是正△ABC的______圆的半径。ABC.OD外接内切半径外接边心距内切4.BOC∠是正△ABC的________角;中心∠BOC=_____度;BOD=_____∠度.120605、正方形ABCD的外接圆圆心O叫做正方形ABCD的____________6、正方形ABCD的内切圆的半径OE叫做正方形ABCD的___________ABCD.OE中心边心距7、⊙O是正五边形ABCDE的外接圆,弦AB的弦心距OF叫正五边形ABCDE的________,它是正五边形ABCDE的________圆的半径。8、∠AOB叫做正五边形ABCDE的_______角,它的度数是________DEABC.OF边心距内切中心72度9、图中正六边形ABCDEF的中心角是_______;它的度数是_________;10、你发现正六边形ABCDEF的半径与边长具有什么数量关系?为什么?BAEFCD.O∠AOB60度11、判断题。、判断题。①①各边都相等的多边形是正多边形。(各边都相等的多边形是正多边形。())②②一个圆有且只有一个内接正多边形(一个圆有且只有一个内接正多边形())22、证明题。、证明题。求证:顺次连结正六边形求证:顺次连结正六边形各边中点所得的多各边中点所得的多边形是正六边形。边形是正六边形。ABCDEF××××ABCDE3.求证:正五边形的对角线相等。证明:在△BCD和△CDE中 BC=CD∠BCD=∠CDECD=DE∴△BCD≌△CDE∴BD=CE同理可证对角线相等。...