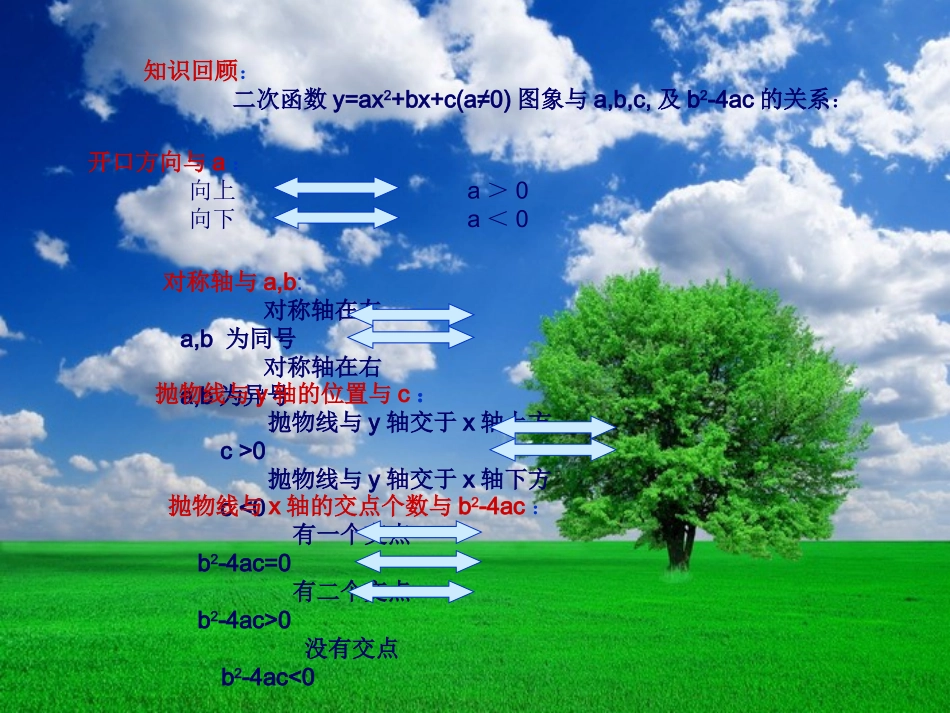
二次函数图象与符号株洲市攸县网岭镇中学王政希二次函数图象与符号学习目标:通过学习,学生能熟练的根据二次函数图象确定其符号。方法与思想:数学方法:比较法,列举法,方程法,代入法。数学思想:函数与方程思想,数形结合思想,分类讨论思想。知识回顾:二次函数y=ax2+bx+c(a≠0)图象与a,b,c,及b2-4ac的关系:开口方向与a:向上a>0向下a<0对称轴与a,b:对称轴在左a,b为同号对称轴在右a,b为异号抛物线与y轴的位置与c:抛物线与y轴交于x轴上方c>0抛物线与y轴交于x轴下方c<0抛物线与x轴的交点个数与b2-4ac:有一个交点b2-4ac=0有二个交点b2-4ac>0没有交点b2-4ac<0已知二次函数y=ax2+bx+c(a≠0)图象如图所示,你能得到哪些信息?1.a-13xyX=1>0,b0,c<0,比如,ab<0,ac<0,bc>0abc>0<3.当x=-1或x=3时,5.当-1<x<3时,ax2+bx+c=0,y=0,把x=-1代入y=ax2+bx+c中,把x=3代入y=ax2+bx+c中,两根之积为c/a=-3,4.b2-4ac>0ax2+bx+c<0,y<0,把x=-2代入y=ax2+bx+c中,把x=4代入y=ax2+bx+c中,2.当x<-1或x>3时,ax2+bx+c>0,y>0,得到4a-2b+c>0得到16a+4b+c>0得到a-b+c=0得到9a+3b+c=0得到c=-3a,c+3a=0把x=1,代入y=ax2+bx+c中,得到a+b+c<0-20已知二次函数y=ax2+bx+c(a≠0)图象如图所示:a___0,b___0,c___0,b2-4ac___00xy<<>>