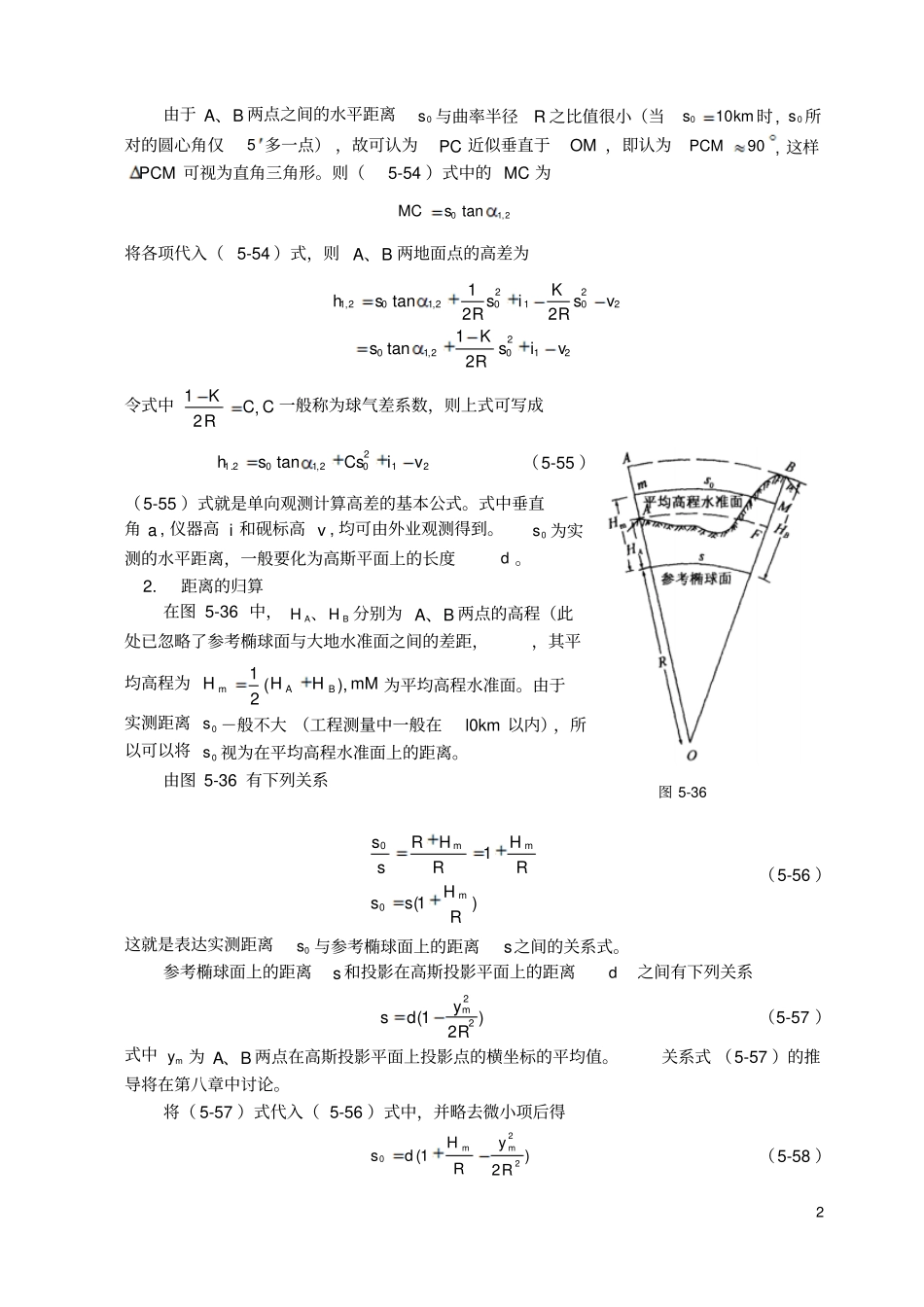
1§5.9三角高程测量三角高程测量的基本思想是根据由测站向照准点所观测的垂直角(或天顶距)和它们之间的水平距离,计算测站点与照准点之间的高差。这种方法简便灵活,受地形条件的限制较少,故适用于测定三角点的高程。三角点的高程主要是作为各种比例尺测图的高程控制的一部分。一般都是在一定密度的水准网控制下,用三角高程测量的方法测定三角点的高程。5.9.1三角高程测量的基本公式1.基本公式关于三角高程测量的基本原理和计算高差的基本公式,在测量学中已有过讨论,但公式的推导是以水平面作为依据的。在控制测量中,由于距离较长,所以必须以椭球面为依据来推导三角高程测量的基本公式。如图5-35所示。设0s为BA、两点间的实测水平距离。仪器置于A点,仪器高度为1i。B为照准点,砚标高度为2v,R为参考椭球面上BA的曲率半径。AFPE、分别为过P点和A点的水准面。PC是PE在P点的切线,PN为光程曲线。当位于P点的望远镜指向与PN相切的PM方向时,由于大气折光的影响,由N点出射的光线正好落在望远镜的横丝上。这就是说,仪器置于A点测得MP、间的垂直角为2,1a。由图5-35可明显地看出,BA、两地面点间的高差为NBMNEFCEMCBFh2,1(5-54)式中,EF为仪器高NBi;1为照准点的觇标高度2v;而CE和MN分别为地球曲率和折光影响。由2021sRCE2021sRMN式中R为光程曲线PN在N点的曲率半径。设,KRR则20202.21SRKSRRRMNK称为大气垂直折光系数。图5-352由于BA、两点之间的水平距离0s与曲率半径R之比值很小(当kms100时,0s所对的圆心角仅5多一点),故可认为PC近似垂直于OM,即认为90PCM,这样PCM可视为直角三角形。则(5-54)式中的MC为2,10tansMC将各项代入(5-54)式,则BA、两地面点的高差为21202,102201202,102,121tan221tanvisRKsvsRKisRsh令式中CCRK,21一般称为球气差系数,则上式可写成21202,102.1tanviCssh(5-55)(5-55)式就是单向观测计算高差的基本公式。式中垂直角a,仪器高i和砚标高v,均可由外业观测得到。0s为实测的水平距离,一般要化为高斯平面上的长度d。2.距离的归算在图5-36中,BAHH、分别为BA、两点的高程(此处已忽略了参考椭球面与大地水准面之间的差距,,其平均高程为mMHHHBAm),(21为平均高程水准面。由于实测距离0s-般不大(工程测量中一般在l0km以内),所以可以将0s视为在平均高程水准面上的距离。由图5-36有下列关系)1(100RHssRHRHRssmmm(5-56)这就是表达实测距离0s与参考椭球面上的距离s之间的关系式。参考椭球面上的距离s和投影在高斯投影平面上的距离d之间有下列关系)21(22Rydsm(5-57)式中my为BA、两点在高斯投影平面上投影点的横坐标的平均值。关系式(5-57)的推导将在第八章中讨论。将(5-57)式代入(5-56)式中,并略去微小项后得)21(220RyRHdsmm(5-58)图5-3633.用椭球面上的边长计算单向观测高差的公式将(5-56)式代入(5-55)式,得2122,12,1)1(tanviCsRHshm(5-59)式中2Cs项的数值很小,故未顾及0s与s之间的差异。4.用高斯平面上的边长计算单向观测高差的公式将(5-57)式代入(5-59)式,舍去微小项后得)2(tan)2(tantan222122,1222,12122,12.1RyRHhviCddRyRHdviCddhmmmm(5-60)式中2,1tandh。令hh2,1)2(22RyRHmm(5-61)则(5-60)式为2,12122,12,1tanhviCddh(5-62)(5-61)式中的mH与R相比较是一个微小的数值,只有在高山地区当mH甚大而高差也较大时,才有必要顾及RHm这一项。例如当mhmHm100,1000时,RHm带这一项对高差的影响还不到0.02m,一般情况下,这一项可以略去。此外,当时mhkmym100,300,222Rym这-项对高差的影响约为0.llm。如果要求高差计算正确到0.lm,则只有hRym222项小于0.04m时才可略去不计,因此,(5-62)式中最后一项2,1h只有当hHm,或my较大时才有必要顾及。5.对向观测计算高差的公式一般要求三角高程测量进行对向观测,也就是在测站A上向B点观测垂直角2,1,而在测站B上也向A点观测垂直角1,2,按(5-62)式有下列两个计算高差的式子。由测站A观测B点2,122,1212,12,1tanhdCvidh则测站B观测A点1,22121,21,21,2tanhdCvidh4式中,11vi、和22vi、分别为A、B点的仪器和觇标高度;2,1C和1,2C为由A观测B和B观测A时的球气差系数。如果观测...