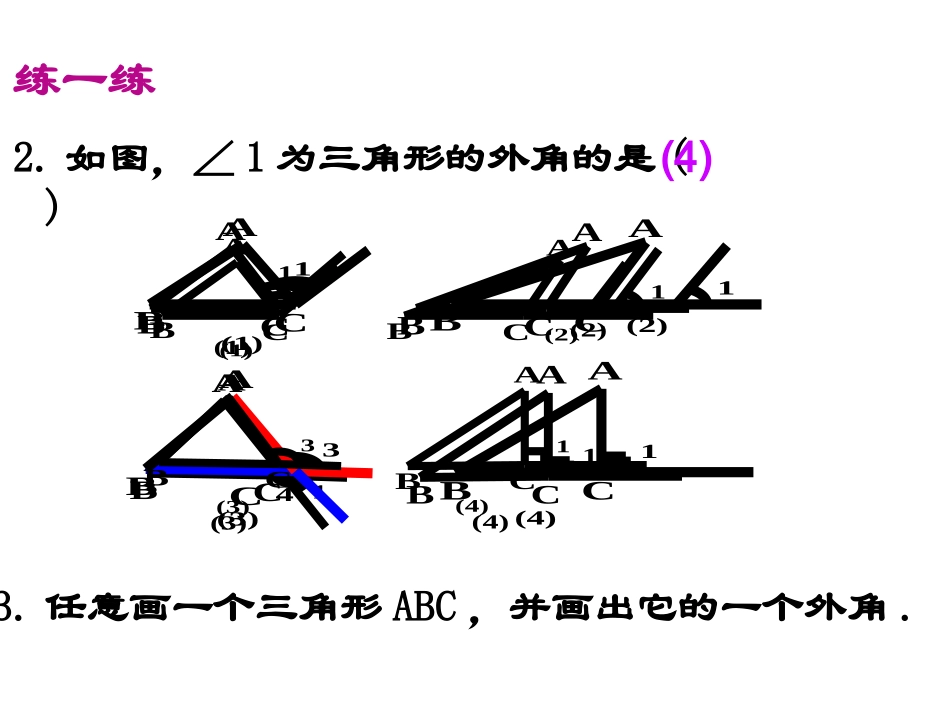
5.三角形内角和定理(2)第七章平行线的证明灵武市第四中学王会霞1.如图△ABC中,∠A=30°,∠B=40°则∠1=.110°三角形的外角定义:三角形内角的一条边与另一条边的反向延长线所组成的角,称为三角形的外角.1BCA21BCDA温故知新练一练2.如图,∠1为三角形的外角的是()(4)3.任意画一个三角形ABC,并画出它的一个外角.(4)(3)(2)(1)1111CCCBBCBBAAAA43(4)(3)(2)(1)111CCCBBCBBAAAA3(4)(3)(2)(1)111CCCBBCBBAAAA∠ACD+∠ACB=180°∠ACD=∠A+B∠∠ACD>A∠∠ACD>B∠结合你画的三角形的外角∠ACD,思考讨论:1.∠ACD与它相邻的内角有什么数量关系?2.∠ACD与不相邻的内角有什么数量关系?3.∠ACD与每个内角有怎样的大小关系?BCDA三角形内角和定理的推论定理:三角形的一个外角等于和它不相邻的两个内角的和.定理:三角形的一个外角大于任何一个和它不相邻的内角.1.已知:如图,在△ABC中,∠A=45°,外角∠DCA=100°,则∠B=,∠ACB=.巩固练习55°80°∴∠BDC>A∠∵∠BDC是△ABD的一个外角2.如图,试比较∠BDC与∠A的大小关系.DCBA例1如图,在三角形ABC中,AD平分外角∠EAC,∠B=C∠.求证:ADBC∥轻松尝试4.还有其他证明方法吗?与同伴交流.思考下列问题,梳理证明思路:1.证明两直线平行的方法有哪些?2.如图示,欲证明ADBC∥,需要找出哪一对角的关系?3.结合已知条件,怎样证明你选择的这对角的关系?5.选择你喜欢的一种方法,将证明过程书写出来.例2已知:如图,P是△ABC内的一点,连接PB、PC.求证:BPC>A.∠∠思考下列问题:1.若要证明两个角的不等关系,我们学过哪些关于角的不等关系的结论?2.如何将∠BPC构造成某个三角形的外角?3.构造后,观察图中哪个角与∠BPC、∠A有不等关系?活动与探究4.还有其他构造三角形的外角方法吗?与同伴交流.1.通过本节课的学习,你获得了哪些知识?2.通过本节课的学习,你学到了哪些方法?3.在应用定理二判断角的大小关系的时候,应注意什么问题?说说这节课你的收获和体验让大家与你分享!本节课主要研究三角形的与的关系.三角形的一个外角大于任何一个和它不相邻的内角.不等量关系:等量关系:三角形的一个外角等于和它不相邻的两个内角的和.内角外角说说这节课你的收获和体验让大家与你分享!课后作业,消化吸收习题7.52、3例2已知:如图,P是△ABC内的一点,连接PB、PC,求证:∠BPC>∠A.PCBADPCBADPCBA例2已知:如图,P是△ABC内的一点,连接PB、PC,求证:∠BPC>∠A.PCBADPCBADPCBA例2已知:如图,P是△ABC内的一点,连接PB、PC,求证:∠BPC>∠A.PCBADPCBADPCBA