函数的最值与导数VIP免费

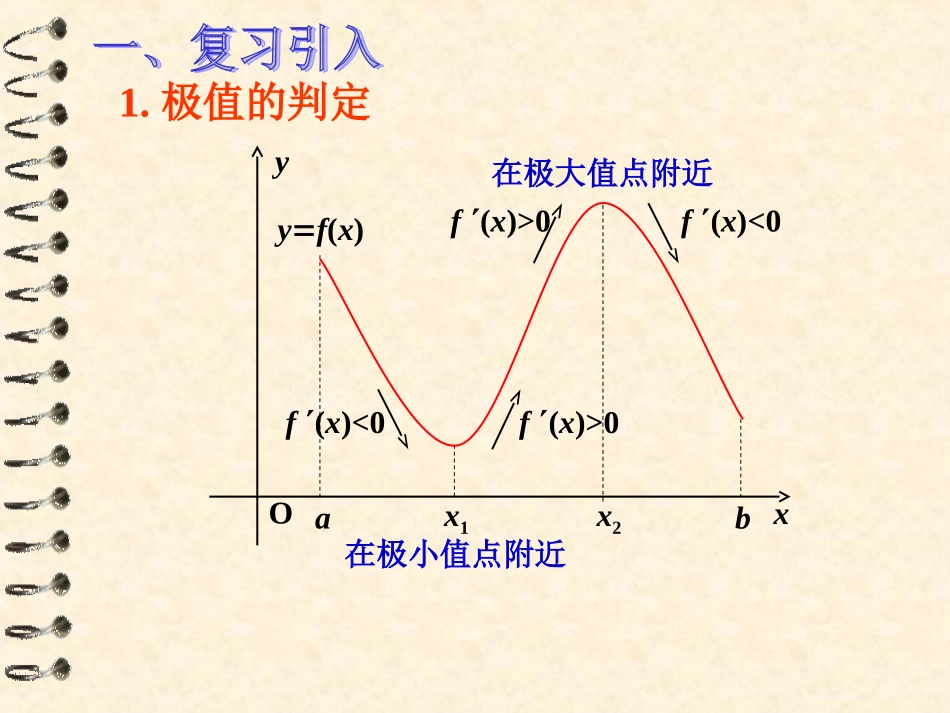
1.3.3函数的最值与导数yxOx1x2abyf(x)在极大值点附近在极小值点附近f(x)<0f(x)>0f(x)>0f(x)<01.极值的判定(1)确定函数的定义域(一般可省)；2.求可导函数f(x)的极值点和极值的步骤：(2)求出导数f´(x)；(3)令f´(x)=0，解方程；(4)列表：把定义域划分为部分区间，考察每个部分区间内f´(x)的符号，判断f(x)的单调性从而确定极值点;(5)下结论，写出极值。xX2oaX3bx1y观察右边一个定义在区间[a,b]上的函数y=f(x)的图象.发现图中____________是极小值，_________是极大值，在区间上的函数的最大值是______，最小值是_______。f(x1)、f(x3)f(x2)f(b)f(x3)问题在于如果在没有给出函数图象的情况下，怎样才能判断出f(x3)是最小值，而f(b)是最大值呢？例1:求y=x3/3-4x+4的极值.解:).2)(2(42xxxy令,解得x1=-2,x2=2.0y当x变化时,,y的变化情况如下表:yx(-∞,-2)-2(-2,2)2(2,+∞)y′y因此,当x=-2时有极大值,并且,y极大值=28/3;而,当x=2时有极小值,并且,y极小值=-4/3.+↗028/3－↘0-4/3+↗在[0,3]的最大值与最小值x0(0,2)2(2,3)3y′y4－↘0-4/3+↗1因此,函数在[0,3]上的最大值是4，最小值是-4/3.求f(x)在[a,b]上的最大值与最小值的步骤如下：①:求y=f(x)在(a，b)内的极值(极大值与极小值);②:将函数y=f(x)的各极值与f(a)、f(b)作比较,其中最大的一个为最大值,最小的一个为最小值.注意1)函数的最值概念是全局性的；2)函数的最大值（最小值）唯一；3)函数的最大值大于等于最小值；4)函数的最值可在端点上取.知识小结：巩固练习1：求函数y=x4-2x2+5在区间[-2,2]上的最大值与最小值.解:.443xxy令,解得x=-1,0,1.0y当x变化时,的变化情况如下表:yy,从上表可知,最大值是13,最小值是4.13↗4↘5↗4↘13y+0-0+0-2(1,2)1(0,1)0(-1,0)-1(-2,-1)-2xy巩固练习2：.[0，2π]上的最值sinx在区间x21求f(x)最小值是0.是π,函数f(x)的最大值xxfcos21)(0)(xf34,3221xx)(xf)(xf234324322343233322332解：令解得x0(0,)(,)+-+00(,)当x变化时,,f(x)的变化情况如下表:)(xf0例2:若函数的最大值为3,最小值为-29,求a,b的值.326012()(),[,]fxaxaxbax解:令得x=0,x=4.23120()fxaxax当x变化时,,f(x)的变化情况如下表:)(xfx-1(-1,0)0(0,2)2f’(x)+0-0f(x)-7a+b↗b↘-16a+b由表知,当x=0时,f(x)取得最大值b,故b=3.又f(-1)-f(2)=9a>0,所以f(x)的最小值为f(2)=-16a+3=-29,故a=2.课堂小结求f(x)在[a,b]上的最大值与最小值的步骤如下：①:求y=f(x)在(a，b)内的极值(极大值与极小值);②:将函数y=f(x)的各极值与f(a)、f(b)作比较,其中最大的一个为最大值,最小的一个为最小值.求函数y=x³+3x²－9x在上［－4,4］的最大值和最小值。解(1)由f´(x)=3x²+6x－9,(2)区间［－4,4］端点处的函数值为f(－4)=20,f(4)=76(3)比较以上各函数值，例2解得x=－3，或x=1f(－3)=27,f(1)=－5可知函数在［－4,4］上的最大值为f(4)=76，最小值为f(1)=－5