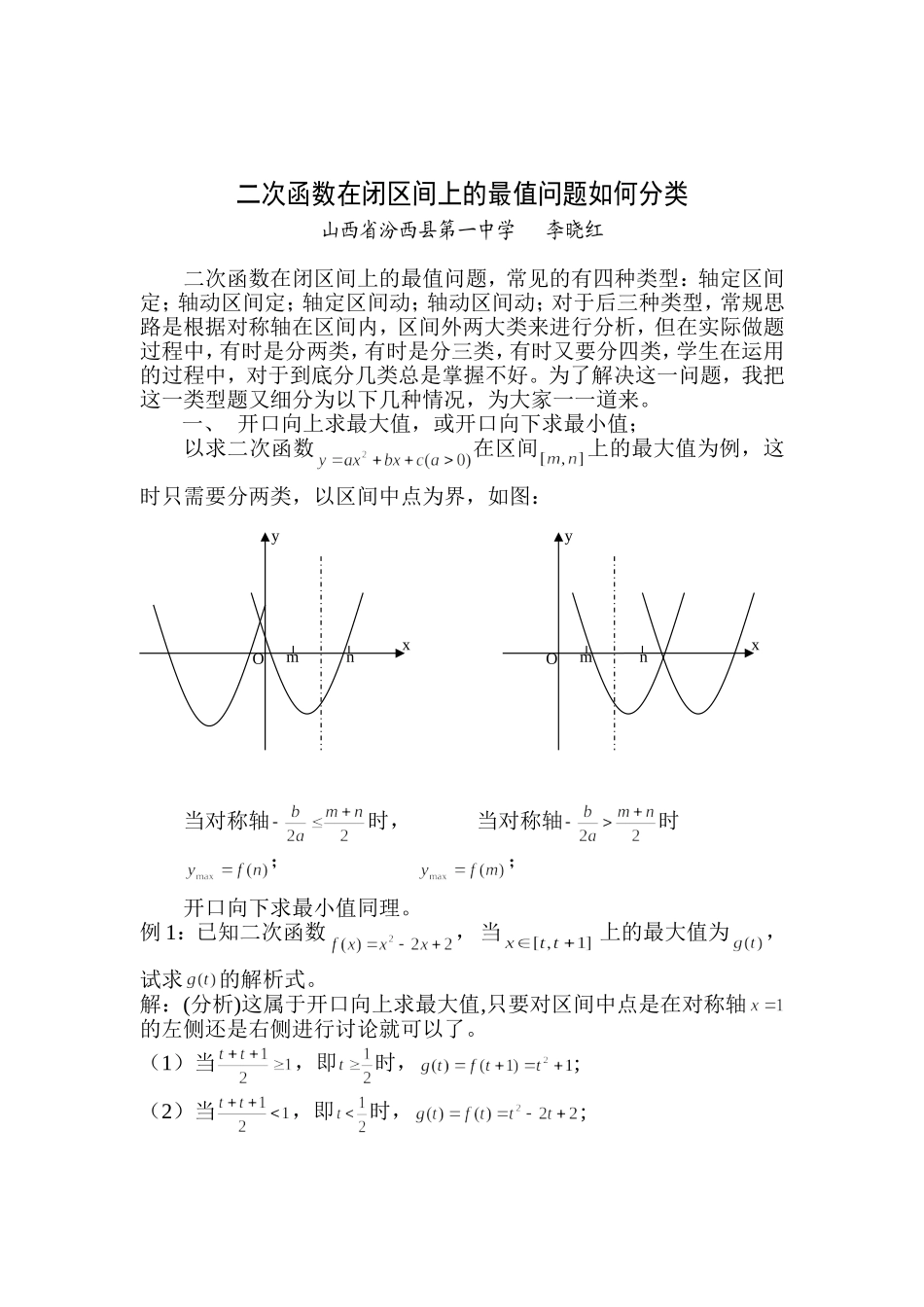
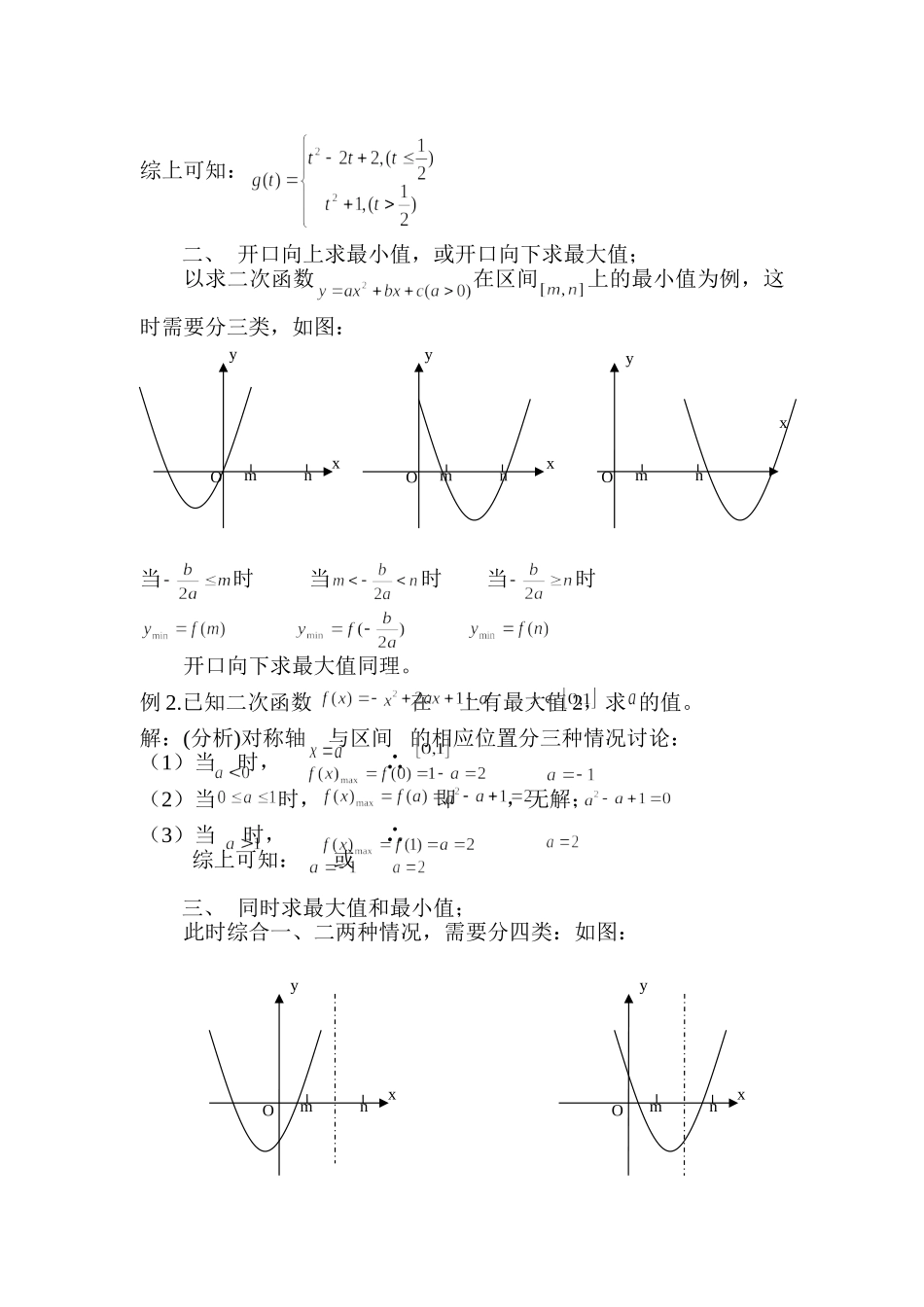
二次函数在闭区间上的最值问题如何分类山西省汾西县第一中学李晓红二次函数在闭区间上的最值问题,常见的有四种类型:轴定区间定;轴动区间定;轴定区间动;轴动区间动;对于后三种类型,常规思路是根据对称轴在区间内,区间外两大类来进行分析,但在实际做题过程中,有时是分两类,有时是分三类,有时又要分四类,学生在运用的过程中,对于到底分几类总是掌握不好。为了解决这一问题,我把这一类型题又细分为以下几种情况,为大家一一道来。一、开口向上求最大值,或开口向下求最小值;以求二次函数在区间上的最大值为例,这时只需要分两类,以区间中点为界,如图:当对称轴时,当对称轴时;;开口向下求最小值同理。例1:已知二次函数,当上的最大值为,试求的解析式。解:(分析)这属于开口向上求最大值,只要对区间中点是在对称轴的左侧还是右侧进行讨论就可以了。(1)当,即时,;(2)当,即时,;mnxyOmnxyO综上可知:二、开口向上求最小值,或开口向下求最大值;以求二次函数在区间上的最小值为例,这时需要分三类,如图:当时当时当时开口向下求最大值同理。例2.已知二次函数在上有最大值2,求的值。解:(分析)对称轴与区间的相应位置分三种情况讨论:(1)当时,∴(2)当时,即,无解;(3)当时,∴综上可知:或三、同时求最大值和最小值;此时综合一、二两种情况,需要分四类:如图:yxmnxyOmnxyOmnOmnmnyxOyxO当时,当时当时,当时例3:已知,当时,求的最小值与最大值.解:由已知可求对称轴为.(1)当时,在上单调递增,.(2)当,即时,.当时,即时,.当时,即时,.(3)当即时,在上单调递减,,.通过以上这三种比较详细的分类,相信同学们在做题的过程中,一看题目就能做到心中有数,即时下笔。以上只是我个人的一点浅见,还有很多不足之处,希望各位同行批评指正。mnmn附:通讯地址:山西省汾西县第一中学,李晓红邮编:031500电话:13753534761工作单位:汾西一中