函数观点看一次函数VIP免费

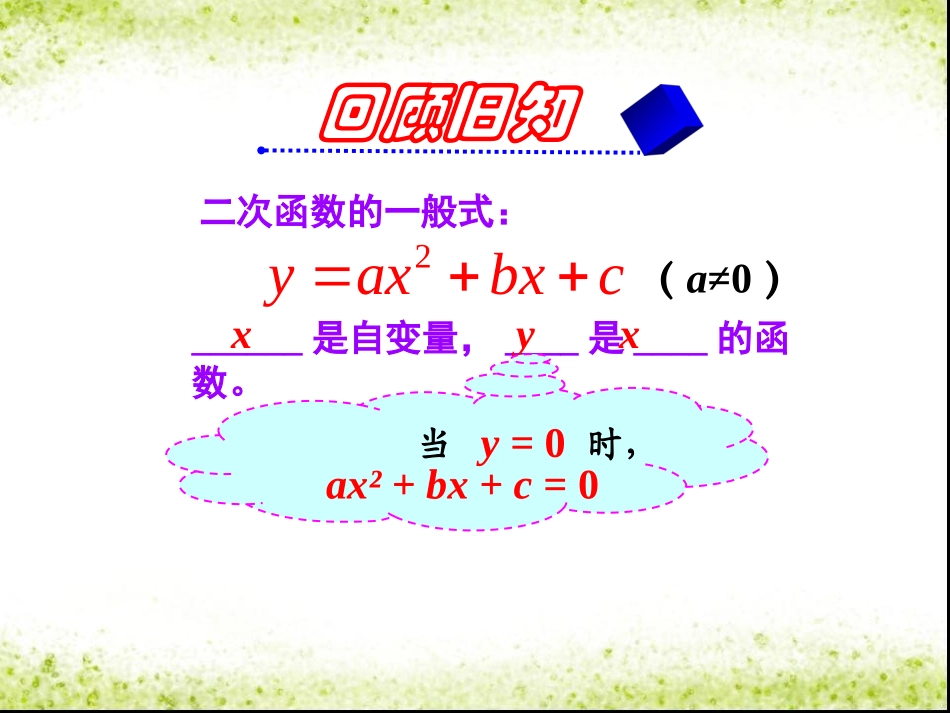
26.2用函数观点看一元二次方程赵付堂回顾旧知2yaxbxc二次函数的一般式：（a≠0）______是自变量，____是____的函数。xyx当y=0时，ax²+bx+c=0学习目标1.理解一元二次方程根的情况与二次函数图像与x轴位置关系的联系；2.会判断二次函数与x轴交点的个数；3.体会数形结合思想的运用。阅读教材p16-p18，回答下列问题：1.请画出函数h=20t–5t2的图像，尝试在图像上找出纵坐标分别为15m,20m,20.5m,0m的点；2.再找出上述各点的横坐标，并说说它表示的实际意义；3.函数h=20t–5t2的图像与t轴的交点的横坐标，与方程20t–5t2=0的根有什么关系？4.二次函数y=ax2+bx+c的图象和x轴交点的横坐标，与一元二次方程ax2+bx+c=0的根有什么关系？下列二次函数的图象与x轴有交点吗?若有，求出交点坐标.（1）y=x2＋x－2（2）y=x2－6x+9（3）y=x2–x+1探究x令y=0，解一元二次方程的根yo-3-2-11234554321-1-2-3●●●有两个根有一个根（两个相同的根）没有根有两个交点有一个交点没有交点b2–4ac>0b2–4ac=0b2–4ac<0二次函数y=ax2+bx+c的图象和x轴交点的三种情况与一元二次方程根的关系ax2+bx+c=0的根y=ax2+bx+c的图象与x轴若抛物线y=ax2+bx+c与x轴有交点，则________________。b2–4ac≥0△＞0△=0△＜0oxy△=b2–4ac随堂练习1.不与x轴相交的抛物线是（）A.y=2x2–3B.y=－2x2+3C.y=－x2–3xD.y=－2(x+1)2－3D2.如果关于x的一元二次方程x2－2x+m=0有两个相等的实数根，则m=＿＿＿，此时抛物线y=x2－2x+m与x轴有＿＿个交点.113.已知抛物线y=x2–8x+c的顶点在x轴上，则c=＿＿.164.若抛物线y=x2+bx+c的顶点在第一象限,则方程x2+bx+c=0的根的情况是＿＿＿＿＿.无实数根5.若抛物线y=ax2+bx+c=0，当a>0，c<0时，图象与x轴交点情况是（）A.无交点B.只有一个交点C.有两个交点D.不能确定C7.抛物线y=2x2－3x－5与y轴交于点＿＿＿＿，与x轴交于点.6.一元二次方程3x2+x－10=0的两个根是x1=-2，x2=5/3，那么二次函数y=3x2+x－10与x轴的交点坐标是＿＿＿＿＿＿＿＿.(0，－5)(5/2，0)(－1，0)(-2，0)(5/3，0)8.已知抛物线y=ax2+bx+c的图象如图,则关于x的方程ax2+bx+c－3=0根的情况是（）A.有两个不相等的实数根B.有两个异号的实数根C.有两个相等的实数根D.没有实数根xAoyx=－13-11.3.9.比一比，看谁完成得又好又快！完成《全效学习》P17.“当堂测评”课堂小结•请谈谈你本节课的收获；•请谈谈你本节课还存在的困惑。•作业：《全效练习》p18-19A组