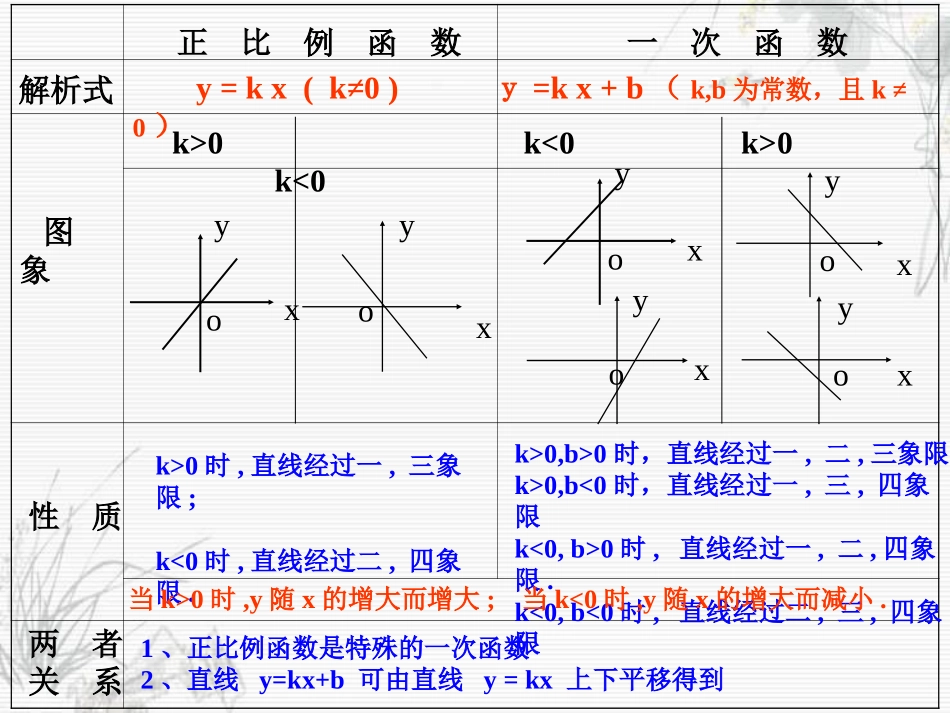
甘溪初级中学李飞杰一次函数图象及性质习题课问题:请用自己的方法把这部分知识整理成好记的体系,也可参照下面的表格完成。(要求:时间5分钟,独立完成;若有困难,可以参阅教材。)一次函数正比例函数解析式图象性质两者关系y=kx(k≠0)y=kx+b(k,b为常数,且k≠0)k>0k<0k>0k<0yxoyxoxyoyxoyxoxyok>0时,直线经过一,三象限;k<0时,直线经过二,四象限.k>0,b>0时,直线经过一,二,三象限k>0,b<0时,直线经过一,三,四象限k<0,b>0时,直线经过一,二,四象限.k<0,b<0时,直线经过二,三,四象限当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.1、正比例函数是特殊的一次函数2、直线y=kx+b可由直线y=kx上下平移得到一次函数巧记顺口溜正比例函数是直线,图象一定过圆点.k的正负是关键,决定直线的象限.正k经过一三限,x增减y增减。负k经过二四限,变化规律正相反。上下平移k不变,由此得到一次线。向上加b向下减,直线经过仨象限。1.已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是()ABCDA2.一次函数y=kx+2的图象经过点(1,1),那么下列说法正确的是()A.K>0B.图象经过原点C.y随x的增大而减小D.图象不经过第二象限C3.一次函数y=-3x+4的图象不经过第____象限。三二k<0、b≥0变式1:一次函数y=kx+b当k>0、b<0时,此函数图象不经过第____象限。变式2:一次函数y=kx+b的图象不经过第三象限,则k、b应满足的条件是____________。4.已知一次函数的图象如右图所示,则此函数的解析式为__________。xy204y=-2x+4变式1:判定下列各点是否在此直线上?A(-3,2)、B(0,2)、C(5,-6)变式2:若点P(4,y)是直线上的一点,求点P的纵坐标y的值。变式3:若点N(x,y)是直线上的一点,且△NOB的面积是2,求点N的坐标。点C(5,-6)在直线上当x=4时,y=2×4﹣+4=-4解:由图象知,点B的坐标是(2,0),且即,|y|=2y=±2∴将y=±2分别代入y=-2x+4中,解得x=1或3∴点N的坐标是(1,2)或(3,2﹣)221yOBSNOBAB解:设函数解析式为y=kx+b,由图象可知,点(2,0)、(0,4)在此直线上,即∴此函数解析式为y=2x+4﹣24024kbbkb解得5.旬阳火车站托运行李费用与托运行李的重量关系如图所示。请你结合图象中的信息解答下列问题。y(元)30203040x(千克)(1)当托运30千克行李时,托运费为_____元;(2)请确定该函数的解析式。(3)当托运行李少于千克,可免费托运。(4)当托运费为44元时,则托运行李千克。2010y=x-1054课外探究:我县为了倡导居民节约用水,生活用自来水按阶梯式水价计费。如图是居民每户每月的水费y(元)与所用的水量x(吨)之间的函数图象。根据下面图象提供的信息,解答下列问题:(1)当10≤x≤25时,求y与x之间的函数关系式;(2)已知某户居民上月水费为55元,求这户居民上月用水多少吨?y/元x/吨01015407025通过这节课的学习,你有什么收获?对同学说,你有什么温馨提示?对老师说,你还有什么困惑?必做题:已知一次函数y=kx+b(k≠0)x=1时,y=5,且它的图象与x轴交点的横坐标是6,求这个一次函数的解析式。选做题:直线y=kx+3与两坐标轴所围成的三角形面积为9,求k的值课后寄语心有多大,舞台就有多大!努力学习,放飞你的梦想!祝愿:同学们期末取得好成绩!解:设一次函数解析式为y=kx+b,把x=1时,y=5;x=6时,y=0代入解析式,得065bkbk解得61bk∴一次函数的解析式为y=-x+6必做题:已知一次函数y=kx+b(k≠0)x=1时,y=5,且它的图象与x轴交点的横坐标是6,求这个一次函数的解析式。课外探究:解:(1)设y=kx+b(10≤x≤25)由图象知:当x=15时,y=40;当x=25时,y=70;则有:解得∴y=3x-5(10≤x≤25)(2)当y=55时,55=3x-5解得x=20∴当水费为55元时,这户居民上月用水20吨。40157025{bkbk35{kb