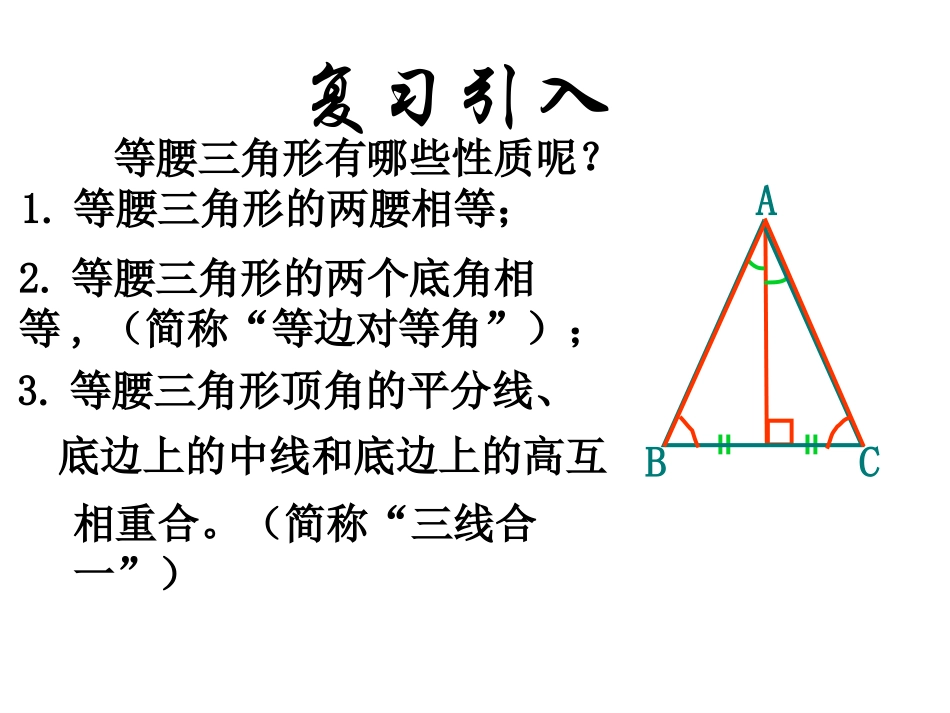
12.3.1等腰三角形的判定峰峰矿区义井中学王玉明复习引入1.等腰三角形的两腰相等;等腰三角形有哪些性质呢?ABC2.等腰三角形的两个底角相等,(简称“等边对等角”);3.等腰三角形顶角的平分线、底边上的中线和底边上的高互相重合。(简称“三线合一”)ABC1.如图:ΔABC中,已知AB=AC,图中有哪些角相等?2.反过来:在ΔABC中,∠B=C∠,那么AB=AC成立吗?∠B=C(∠等腰三角形中等边对等角.)已知:如图,在△ABC中,∠B=C∠。求证:AB=ACABCD12作BC边上的中线或高可以吗?∴∠1=∠2, ∠1=∠2,∠B=∠C,AD=AD,∴△BADCAD≌△(AAS)∴AB=AC(全等三角形的对应边相等)在△BAD和△CAD中,证明:作∠BAC的平分线AD.等腰三角形有以下的判定方法:(2)判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等.简写成:等角对等边.(1)定义法:有两边相等的三角形是等腰三角形。巩固练习证明:1.已知:如图,AD∥BC,BD平分∠ABC,求证:AB=ADABDC ADBC∥∴∠ADB=∠DBC(两直线平行,内错角相等) BD平分∠ABC∴∠ABD=∠DBC(角平分线定义)∴∠ABD=∠ADB(等量代换∴AB=AD(等角对等边)作业:课本P82第5题§14.1.4整式的乘法-------单项式乘多项式峰峰矿区义井中学王玉明单项式乘多项式法则单项式乘多项式法则单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.巩固练习一.判断××1.m(a+b+c+d)=ma+b+c+d()2321112.(2)1222aaaaa()3.(-2x)•(ax+b-3)=-2ax2-2bx-6x()×1.单项式与多项式相乘,就是用单项式去乘多项式的________,再把所得的积________二.填空2.4(a-b+1)=___________________每一项相加4a-4b+43.3x(2x-y2)=___________________6x2-3xy24.-3x(2x-5y+6z)=___________________-6x2+15xy-18xz5.(-2a2)2(-a-2b+c)=___________________-4a5-8a4b+4a4c(-2ab)3(5a2b–2b3)解:原式=(-8a3b3)(5a2b–2b3)=(-8a3b3)·(5a2b)+(-8a3b3)·(-2b3)=-40a5b4+16a3b6说明:说明:先进行乘方运算,再进行先进行乘方运算,再进行单项式与多项式的乘法运算。单项式与多项式的乘法运算。三、例3、计算:例4计算:-2a2·(ab+b2)-5a(a2b-ab2)解:原式=-2a3b-2a2b2-5a3b+5a2b2=-2a3b-2a2b2-5a3b+5a2b2注意:1.将--2a2与--5a的“--”看成性质符号2.单项式与多项式相乘的结果中,应将同类项合并。=-7a3b+3a2b2单项式与多项式相乘时,分三个阶段:单项式与多项式相乘时,分三个阶段:①按乘法分配律把乘积写成单项式与单项式乘积的代数和的形式;②单项式的乘法运算;③再把所得的积相加.几点注意:几点注意:1.单项式乘多项式的结果仍是多项式,积的项数与原多项式的项数相同。2.单项式分别与多项式的每一项相乘时,要注意积的各项符号的确定:同号相乘得正,异号相乘得负.3.不要出现漏乘现象,运算要有顺序。y2(y2+9y-12)–3(3y3-4y2),其中y=-3.解:y2(y2+9y-12)–3(3y3-4y2)=y4+9y3-12y2–9y3+12y2=y4当y=-3时,原式=(-3)4=81例5化简求值:这节课你有什么收获?一、单项式与多项式相乘法则单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.1.单项式乘多项式的结果仍是多项式,积的项数与原多项式的项数相同。2.单项式分别与多项式的每一项相乘时,要注意积的各项符号的确定:同号相乘得正,异号相乘得负.3.不要出现漏乘现象,运算要有顺序。二、单项式与多项式相乘注意事项单项式与多项式相乘注意事项二、单项式与多项式相乘注意事项单项式与多项式相乘注意事项(-2a)•(2a2-3a+1)=(-2a)•2a2=-4a3+6a2-2a(乘法分配律)(乘法分配律)(单项式与单项式相乘法则)(单项式与单项式相乘法则)(-2a)•(-3a)(-2a)•1++++我思,我进步223x+5y+2zx2+2x+18t-5221rab单项式单项式+判断判断::下列代数式哪些是多项式下列代数式哪些是多项式??.,12,31,222yxyxxyxa④③②①:多项式有,12x.22yxyx单项式和多项式统称整式解剖多项式解剖多项式如a2-3a-2的项分别有,常数项是____,最高次项的次数是_____。∴a2-3a-2为二次三项式。aa22,-3a,-2,-3a,-2-2-222在多项式中,每个单项式叫做多项式的项不含字...