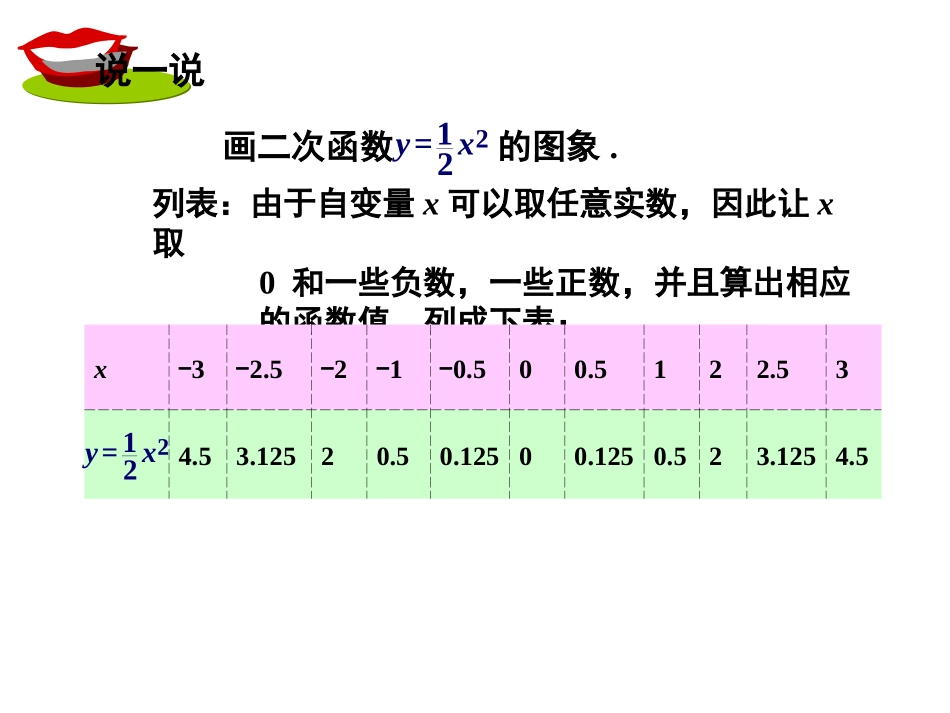
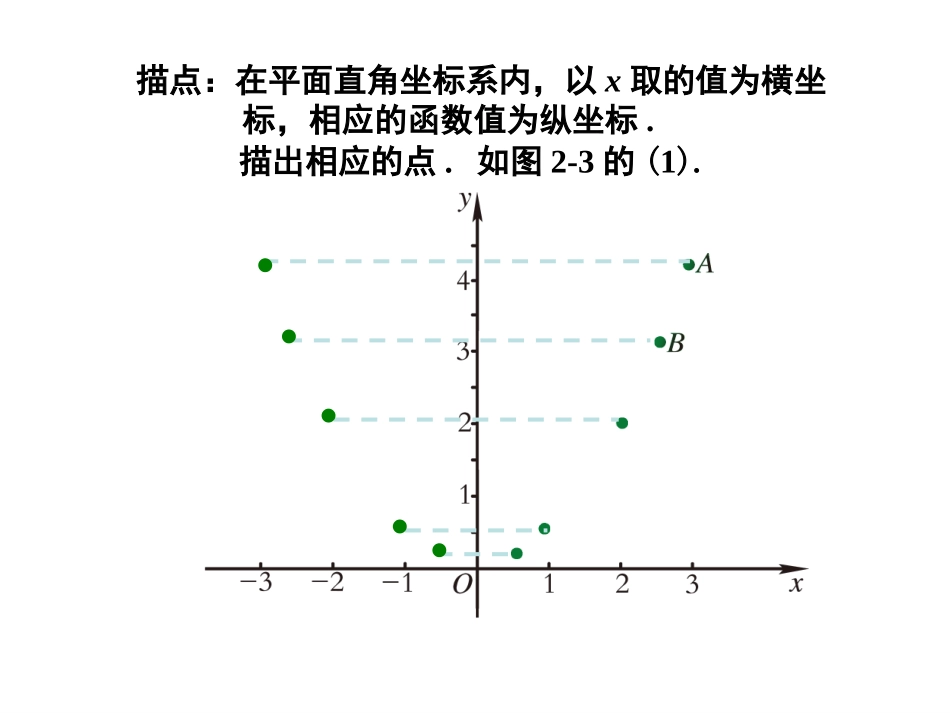
二次函数的图象与性质1说一说画二次函数的图象.21=2yx列表:由于自变量x可以取任意实数,因此让x取0和一些负数,一些正数,并且算出相应的函数值,列成下表:x-3-2.5-2-1-0.500.5122.534.53.12520.50.12500.1250.523.1254.521=2yx描点:在平面直角坐标系内,以x取的值为横坐标,相应的函数值为纵坐标.描出相应的点.如图2-3的(1).观察和分析:从图2-3的(1)看出,点A和点A′,点B和点B′,…,它们有什么关系?ABA′B′点A和点A′关于y轴对称,点B和点B′也是……点A和点A′关于y轴对称,点B和点B′也是……由此你能作出什么猜测?由此你能作出什么猜测?我猜测的图象关于y轴对称.我猜测的图象关于y轴对称.21=2yx从图2-3的(1)还可看出,y轴右边描出的各点,当横坐标增大时,纵坐标怎样变化?纵坐标随着增大.纵坐标随着增大.的图象在y轴右边的所有点都具有这样的性质吗?21=2yx我猜想都有这一性质.我猜想都有这一性质.的图象在y轴右边的所有点都具有这样的性质吗?21=2yx可以证明上述两个猜测都是正确的,即的图象关于y轴对称;图象在y轴右边的部分,函数值随自变量取值的增大而增大,简称为“右升”.21=2yx连线:根据上述分析,我们可以用一条光滑曲线把原点和y轴右边各点顺次连接起来;然后利用对称性,画出图象在y轴左边的部分(把y轴左边的对应点和原点用一条光滑曲线顺次连接起来),这样就得到了的图象.如图2-3的(2).21=2yx观察我们已经正确地画出了的图象,因此,现在可以从图象(见图2-3的(2))看出的其他一些性质(除了上面已经知道的关于y轴对称和“右升”外):21=2yx21=2yx对称轴与图象的交点是;图象的开口向;图象在对称轴左边的部分,函数值随自变量取值的增大而,简称为“左降”;当x=时,函数值最.O(0,0)上减小0小对称轴与图象的交点是;图象的开口向;图象在对称轴右边的部分,函数值随自变量取值的增大而,简称为“右升”;当x=时,函数值最.O(0,0)上减小0小教师归纳:类似地,当a>0时,y=ax2的图象也具有上述性质.图象是轴对称图形,对称轴是_______图象在对称轴左边的部分,函数值随自变量取值的增大而,简称为“左降”;二次函数的图象是抛物线,)0(2aaxyY轴增大于是我们在画y=ax2(a>0)的图象时,可以先画出图象在y轴右边的部分,然后利用对称性,画出图象在y轴左边的部分.在画右边部分时,只要“列表、描点、连线”三个步骤就可以了(因为我们知道了图象的性质).例1画二次函数y=x2的图象.举例解列表:x00.511.523y=x200.2512.2549描点和连线:画出图象在y轴右边的部分.如图利用对称性,画出图象在y轴左边的部分.这样我们得到了y=x2的图象.如图2.二次函数y=6x2的性质有:(1)对称轴是;(2)图象的开口向;(3)图象在对称轴右边的部分,函数值随自变量取值的增大而;在对称轴左边的部分,函数值随自变量取值的增大而.x=0上增大减小3.在同一直角坐标系中画出二次函数y=2x2及的图象.21=4yx3.比较函数y=2x2的图象与的图象,有什么共同点和不同点?21=4yx答:对称轴相同,均为x=0;图象的开口方向均向上;函数y=2x2的图象的开口比的开口窄;有相同的增、减性.21=4yx4、已知是二次函数,且当X>0时,Y随X的增大而增大。(1)求函数解析式;(2)求函数图象的对称轴和顶点坐标42)2(kkxky5、已知抛物线经过点A(2,8)(1)求此抛物线的函数解析式;(2)判断点B(1,4)是否在此抛物线上;(3)求出此抛物线上纵坐标为6的点的坐标。2axy小结:作业:全品14页13题