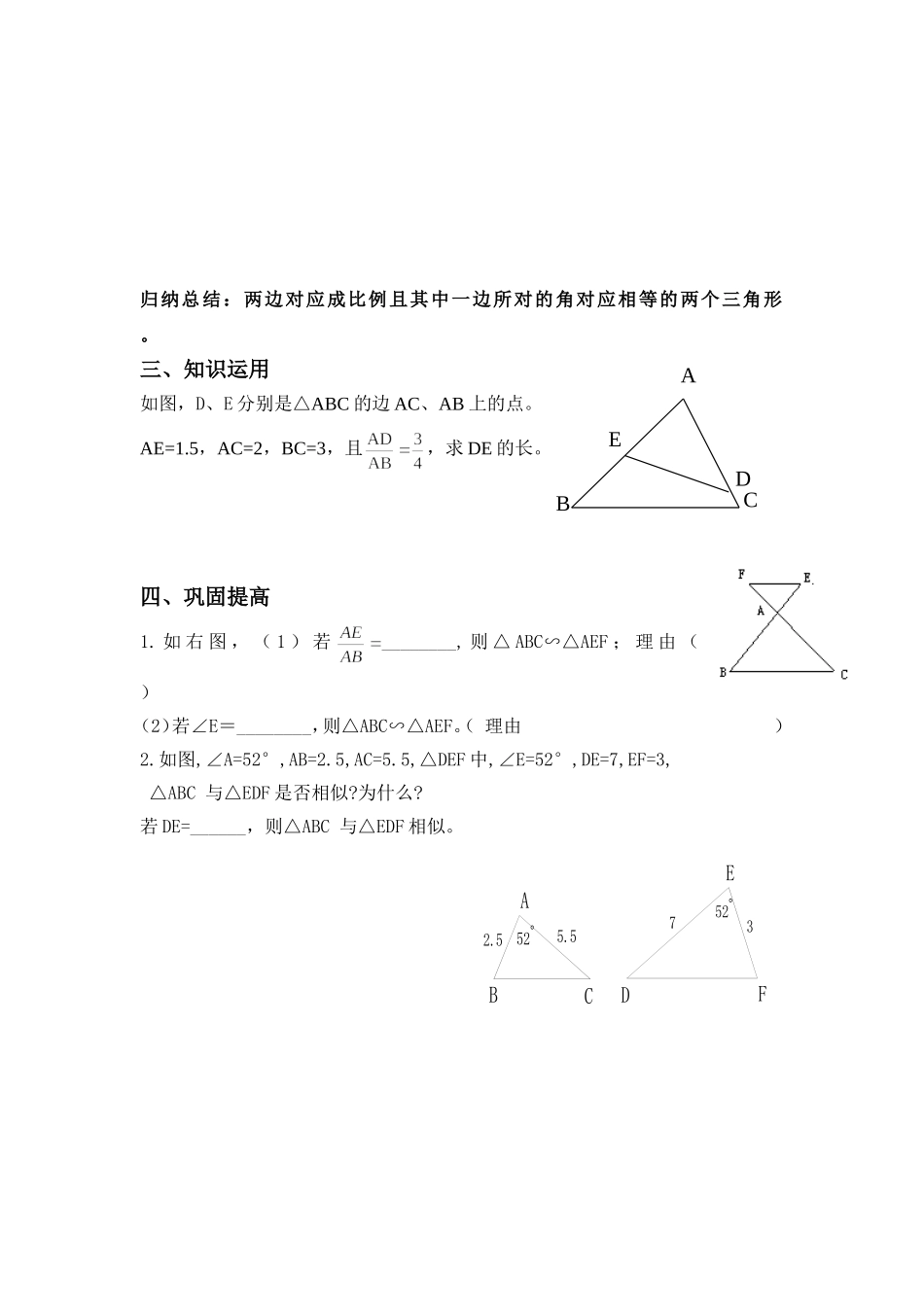
4.4.2探索相似的条件导学案(2)班级:_______姓名:_______月日教学重点:掌握定理:“两边对应成比例且夹角相等的两个三角形相似”。教学难点:相似三角形判定定理在实际问题中的灵活运用一、知识回顾:1.相似三角形的相关概念(1)三个角对应_______、三条边对应_______的两个三角形叫做相似三角形(2)相似三角形的对应角_____,各对应边________.(3)相似比等于______的两个三角形全等.2.(1)全等三角形有哪些判定方法?类比三角形全等的判定,你认为可能还有哪些方法能判定两个三角形相似?(请大胆猜想)(2)两个三角形有两边成比例,它们一定相似吗?(3)如果再增加一个条件,你能说出有哪几种可能的情况吗?(4)如果增加一角相等,你能说出有哪几种可能的情况吗?二、合作探究⑴以两位同学为一小组,画△ABC与△A’B’C’,一位同学作6cm、9cm、为边且夹角为60°的三角形;另一位同学作4cm、6cm、为边且夹角为60°的三角形。⑵然后同桌进行对照,观察两个三角形是否相似?归纳总结:两边成比例且夹角相等的两个三角形相似。(3)如果△ABC与△A’B’C’两边成比例,且其中一边所对的角相等,那么这两个三角形一定相似吗?由此你能得到什么结论?50°)4ABC3.2250°)1.6EDF归纳总结:两边对应成比例且其中一边所对的角对应相等的两个三角形。三、知识运用如图,D、E分别是△ABC的边AC、AB上的点。AE=1.5,AC=2,BC=3,且,求DE的长。四、巩固提高1.如右图,(1)若________,则△ABC∽△AEF;理由()(2)若∠E=________,则△ABC∽△AEF。(理由)2.如图,∠A=52°,AB=2.5,AC=5.5,△DEF中,∠E=52°,DE=7,EF=3,△ABC与△EDF是否相似?为什么?若DE=______,则△ABC与△EDF相似。525.52.5CBA5237DEFAEDCB