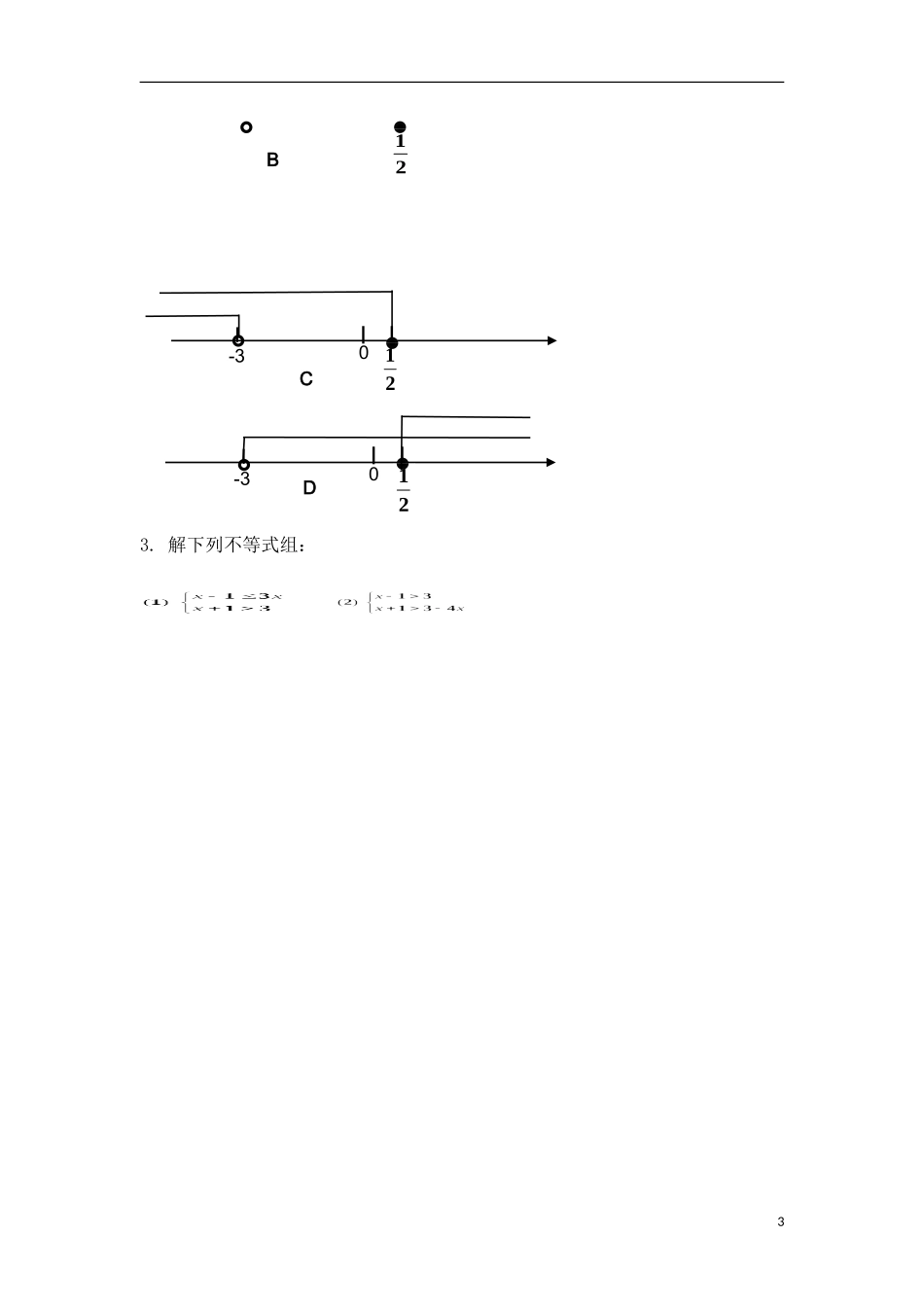
一元一次不等式组及其解法一、教学目标:1.了解一元一次不等式组及其解集的概念.2.探索不等式组的解法及其步骤.3.结合数轴,熟练地解一元一次不等式组.二、重点、难点分析:重点:一元一次不等式组的解法难点:正确理解不等式组的解集三、教学方法:类比、讲练结合四、教学过程(一)复习导入:解下列不等式,并将其解集在数轴上表示出来:(1)2x-1>x+1(2)x+8<4x-1(二)形成概念2x-1>x+1将(1)(2)合在一起,组成一个一元一次不等式组.x+8<4x-1概念:由几个(两个或两个以上)含有相同未知数的一元一次不等式合起来构成的不等式组,叫做一元一次不等式组.注意:(1)每个不等式必须为一元一次不等式(2)不等式必须是只含有同一个未知数(3)不等式的数量是两个或两个以上观察与思考:下列各式中,哪些是一元一次不等式组?(三)解集探究2x-1>x+1①1.试着在同一数轴上表示出不等式①、②的解集.x+8<4x-1②概括:几个不等式的解集的公共部1分,叫做由它们所组成的不等式组的解集.求不等式组的解集的过程,叫做解不等式组.例1解下列不等式组归纳:解一元一次不等式组,通常可以先分别求出不等式组中每一个不等式的解集,再求出它们的公共部分.利用数轴可以直观地帮助我们求出不等式组的解集.你会了吗?2.试一试:你会找公共部分吗?第一种第二种第三种第四种归纳得口决:同大取大,同小取小,大小小大取中间,大大小小无解.3.解下列不等式组,并把解集表示在数轴上:(四)小结:1.不等组的解集的意义.2.数形结合,借助数轴来确定解集.(五)布置作业(六)强化训练1.不等式组的解集为()A.B.C.D.无解2.不等式组的解集在数轴上可表示为()21x3x13x0-3A210-33.解下列不等式组:321B0-3C210-3D21