一元二次方程根与系数关系-(2)VIP免费

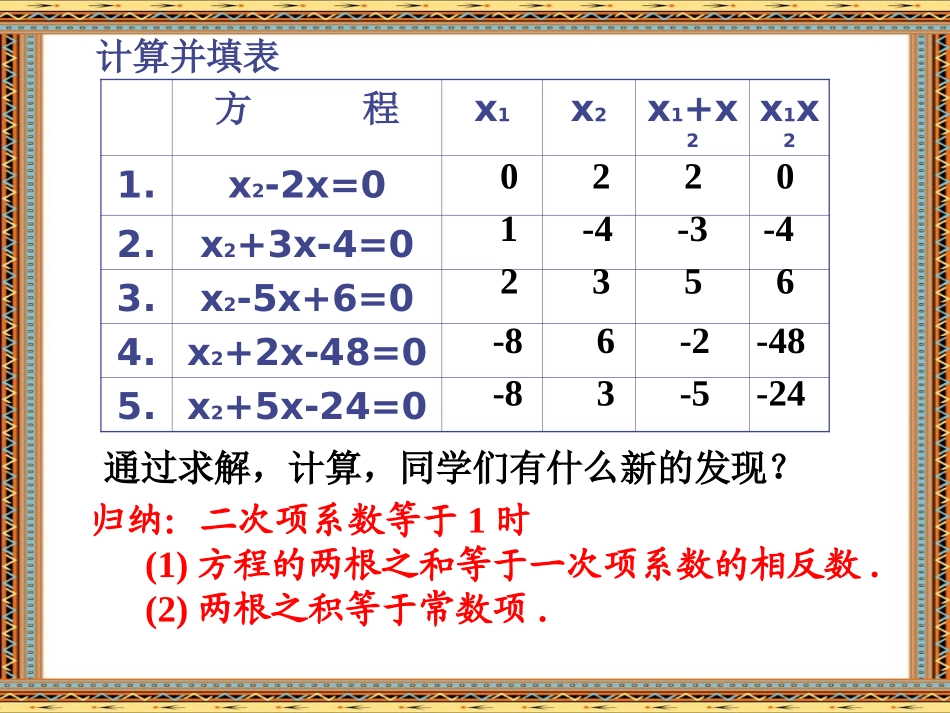
第一课时学习目标1.经历和体验数学发现的过程，提高学生的思维品质和进行探究学习的能力，从中获得学习的快乐。2.掌握一元二次方程的根与系数的关系；3.会用一元二次方程的根与系数的关系解决简单的问题。方程x1x2x1+x2x1x21.x2-2x=02.x2+3x-4=03.x2-5x+6=04.x2+2x-48=05.x2+5x-24=002201-4-3-42356-86-2-48-83-5-24归纳：二次项系数等于1时(1)方程的两根之和等于一次项系数的相反数.(2)两根之积等于常数项.通过求解，计算，同学们有什么新的发现？计算并填表关于x的方程+bx+c=0两根为x1,x2(b,c为常数).则：x1+x2=,x1x2=x2一元二次方程根与系数的关系(1).当二次项系数为1的时候-bc探索：若二次项的系数不等于1时，他们又有什么关系，请同学们尝试一下.方程x1x2x1+x2x1x21.2x2-x-6=02.2x2+x-6=03.5x2-4x-12=02-3/21/2-3-23/2-1/2-3-6/524/5-12/5归纳：(2)关于x的方程两根为,则,002acbxax21,xxacxxabxx2121,新授20(0)axbxca221244,22bbacbbacxxaa1212??xxxx在使用根与系数的关系时，应注意：⑴不是一般式的要先化成一般式；⑵在使用X1+X2=－时，注意“－”不要漏写。ab如果方程ax2+bx+c=0(a≠0)的两个根是X1,X2,那么X1+X2=,X1·X2=ab-ac注：能用根与系数的关系的前提条件为b2-4ac≥0设x1、x2是下列一元二次方程的两个根，填写下表x1·x2x1+x2一元二次方程0652xx03522xx0262xx5625233161（1）x2-6x-7=0（-1，7）（2）3x2+5x-2=0（5/3，-2/3）（3）2x2-3x+1=0（3，1）2.判断下列各方程后面的两个数是不是它的两个根。（口答）练习已知关于x的方程012)1(2mxmx当m=时,此方程的两根互为相反数.当m=时,此方程的两根互为倒数.－11分析:1.0121mxx2.11221mxx引申：1、若ax2bxc0(a00)（1）若两根互为相反数，则b0；（2）若两根互为倒数，则ac；（3）若一根为0，则c0；（4）若一根为1，则abc0；（5）若一根为1，则abc0；（6）若a、c异号，方程一定有两个实数根.例1.不解方程，求方程3x2+2x-9=0的两根(1)倒数和，(2)平方和，(3)差的平方.解：设方程的两根为x1,x2.即x1+x2=-2/3,x1x2=-39233211.1212121xxxxxx9466942.2212212221xxxxxx941212944.321221221xxxxxx解：由根与系数的关系得X1+X2=-k，X1×X2=k+2又X12+X22=4即(X1+X2)2-2X1X2=4K2-2(k+2）=4K2-2k-8=0∵△=K2-4k-8当k=4时，△＜0当k=-2时，△＞0∴k=-2解得：k=4或k=－2例题2、已知方程的两个实数根是且求k的值．022kkxx2,1xx42221xx的值求它的另一个根及，的一个根是：已知方程：例kkxx2,06512解：设方程的另一个根为x1，那么1162535325535275375xxkkk又所以，方程的另一根是，的值是。一元二次方程根与系数的关系：注：能用根与系数的关系的前提条件为b2-4ac≥0关于x的方程两根为,则,002acbxax21,xxacxxabxx2121,数学就是这样一种学问；她要求我们扎扎实实地学习，勤勤恳恳地探索。她提醒你有无形的灵魂，她赋予她所发现的真理以生命；她唤起心神，澄清智能；她给我们的内心思想添辉，她涤尽我们有生以来的蒙昧与无知。关于两根几种常见的求值2111.4xx2121xxxx)1)(1.(321xx1)(2121xxxx1221.5xxxx212221xxxx21212212)(xxxxxx21.6xx221)(xx212214)(xxxx212xx2221.1xx221)(xx221).(2xx221)(xx214xx