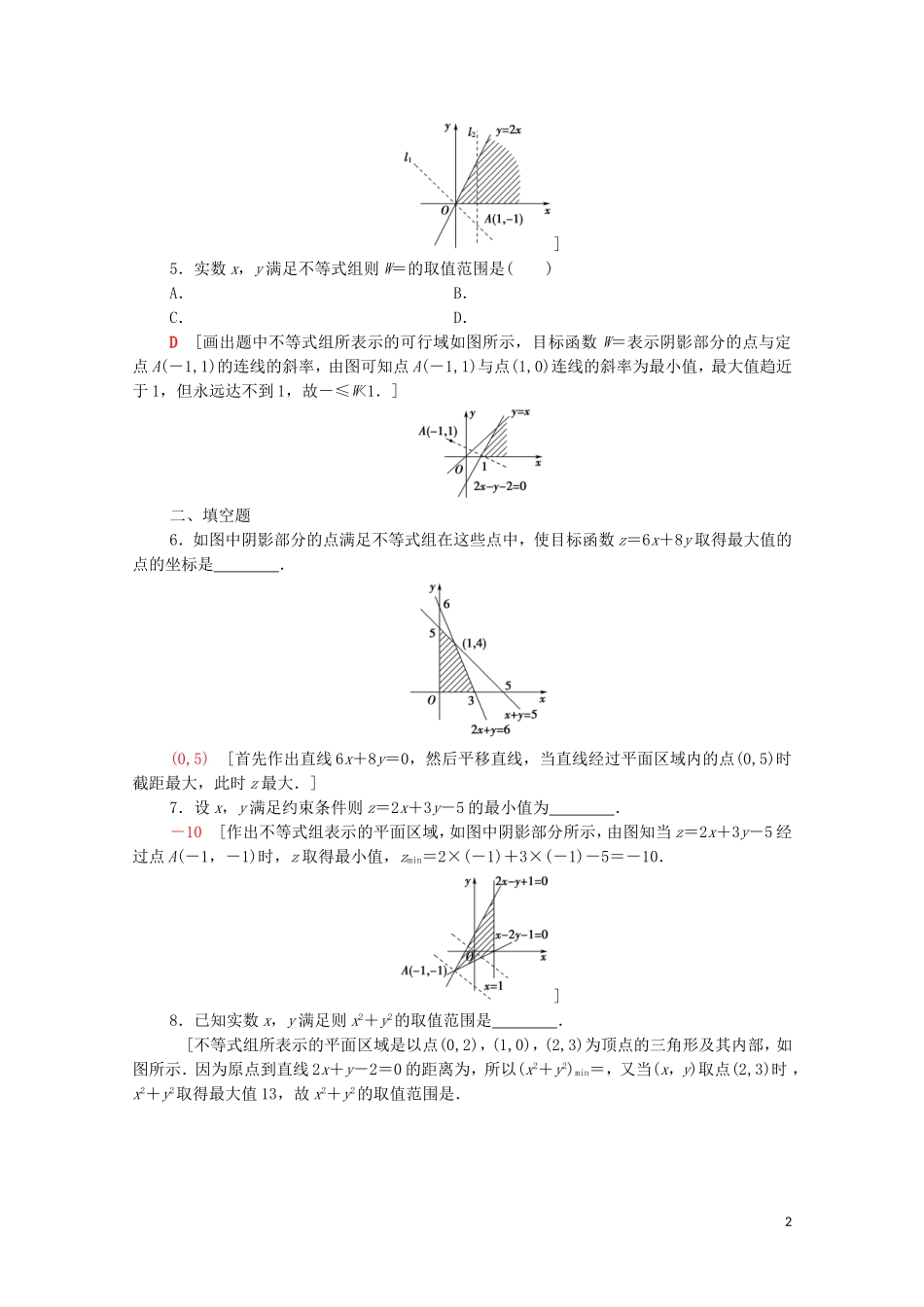
课时分层作业(二十一)简单线性规划(建议用时:60分钟)一、选择题1.不等式组表示的平面区域是()A.矩形B.三角形C.直角梯形D.等腰梯形B[不等式组⇔或那么利用不等式表示的区域可知,得到的区域为三角形,故选B.]2.若x,y∈R,且则z=x+2y的最小值等于()A.2B.3C.5D.9B[可行域如图阴影部分所示,则当直线x+2y-z=0经过点M(1,1)时,z=x+2y取得最小值,为1+2=3.]3.在平面直角坐标系xOy中,M为不等式组所表示的区域上一动点,则直线OM斜率的最小值为()A.2B.1C.-D.-C[如图所示,所表示的平面区域为图中的阴影部分.由得A(3,-1).当M点与A重合时,OM的斜率最小,kOM=-.]4.在平面直角坐标系中,若不等式组表示一个三角形区域,则实数k的取值范围是()A.(-∞,-1)B.(-1,2)C.(-∞,-1)∪(2,+∞)D.(2,+∞)A[作出不等组表示的平面区域,如图中阴影部分所示,注意到直线y=k(x-1)-1恒过点A(1,-1),要使题中不等式组表示的区域为三角形区域,首先必须使k<0(因为若k≥0,则不可能得到三角形区域),然后考虑两临界状态,即图中的直线l1与l2,易得k的取值范围是(-∞,-1).1]5.实数x,y满足不等式组则W=的取值范围是()A.B.C.D.D[画出题中不等式组所表示的可行域如图所示,目标函数W=表示阴影部分的点与定点A(-1,1)的连线的斜率,由图可知点A(-1,1)与点(1,0)连线的斜率为最小值,最大值趋近于1,但永远达不到1,故-≤W<1.]二、填空题6.如图中阴影部分的点满足不等式组在这些点中,使目标函数z=6x+8y取得最大值的点的坐标是.(0,5)[首先作出直线6x+8y=0,然后平移直线,当直线经过平面区域内的点(0,5)时截距最大,此时z最大.]7.设x,y满足约束条件则z=2x+3y-5的最小值为.-10[作出不等式组表示的平面区域,如图中阴影部分所示,由图知当z=2x+3y-5经过点A(-1,-1)时,z取得最小值,zmin=2×(-1)+3×(-1)-5=-10.]8.已知实数x,y满足则x2+y2的取值范围是.[不等式组所表示的平面区域是以点(0,2),(1,0),(2,3)为顶点的三角形及其内部,如图所示.因为原点到直线2x+y-2=0的距离为,所以(x2+y2)min=,又当(x,y)取点(2,3)时,x2+y2取得最大值13,故x2+y2的取值范围是.2]三、解答题9.已知f(x)=(3a-1)x+b-a,x∈[0,1],若f(x)≤1恒成立,求a+b的最大值.[解]因为f(x)≤1在[0,1]上恒成立,所以即将a,b对应为平面aOb上的点(a,b),则其表示的平面区域如图所示,其中A,求a+b的最大值转化为在约束条件下,目标函数z=a+b的最值的线性规划问题,作直线a+b=0,并且平移使它通过可行域内的A点,此时z=a+b取得的最大值为.10.若实数x,y满足求:(1)z=2x+y的最小值;(2)z=x2+y2的取值范围;(3)z=的最大值.[解]作出满足已知条件的可行域为△ABC内(及边界)区域,如图所示,其中A(1,2),B(2,1),C(3,4).(1)目标函数z=2x+y,表示直线l:y=-2x+z,z表示该直线的纵截距,当l过点A时纵截距有最小值,故zmin=4.(2)目标函数z=x2+y2表示区域内的点到坐标系原点的距离的平方,又原点O到AB的距离d==,且垂足D,在线段AB上,故OD2≤z≤OC2,即z∈,25.(3)目标函数z=+1,记k=.则k表示区域中的点与坐标原点连线的斜率,当直线过点A时,斜率最大,则kmax=2,即zmax=max=3.31.已知x,y满足目标函数z=2x+y的最大值为7,最小值为1,则b,c的值分别为()A.-1,4B.-1,-3C.-2,-1D.-1,-2D[由题意知,直线x+by+c=0经过直线2x+y=7与直线x+y=4的交点,且经过直线2x+y=1和直线x=1的交点,即经过点(3,1)和点(1,-1),∴解得]2.已知x,y满足约束条件使z=x+ay(a>0)取得最小值的最优解有无数个,则a的值为()A.-3B.3C.-1D.1D[如图,作出可行域,作直线l:x+ay=0,要使目标函数z=x+ay(a>0)取得最小值的最优解有无数个,则将l向右上方平移后与直线x+y=5重合,故a=1,选D.]3.已知平面直角坐标系xOy上的区域D由不等式组给定.若M(x,y)为D上的动点,点A的坐标为(,1),则z=OM·OA的最大值为.4[由线性约束条件画出可行域如图中阴影部分所示,目标函数z=OM·OA=x+...