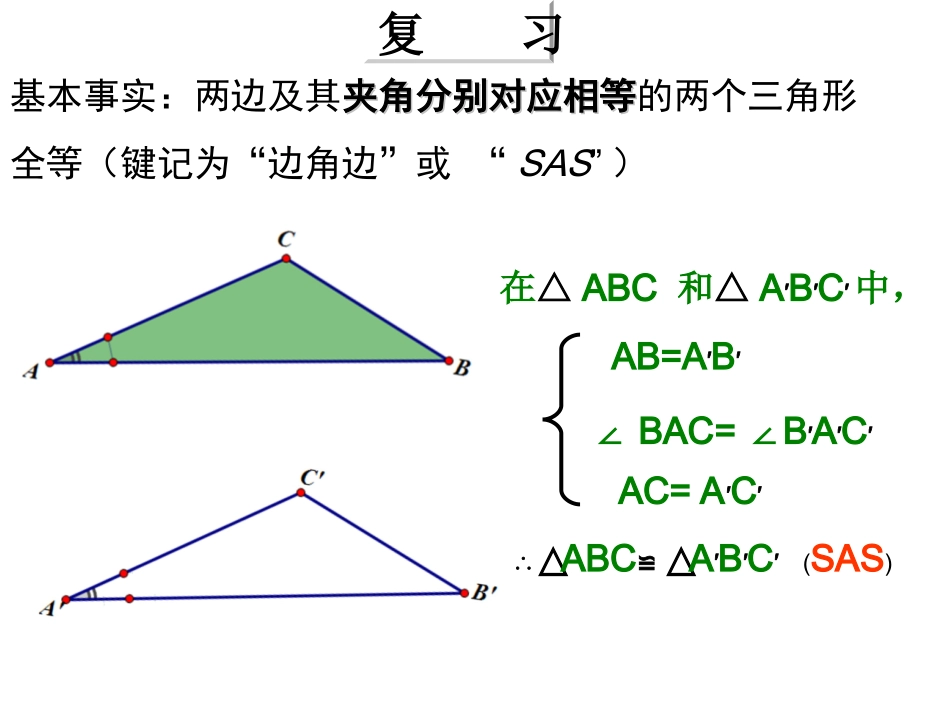
14.2.2三角形全等的判定(角边角—ASA)天峰初中顾传如1.什么是全等三角形?2.判定两个三角形全等要具备什么条件?复习边角边:有两边和它们夹角对应相等的两个三角形全等。基本事实:两边及其夹角分别对应相等夹角分别对应相等的两个三角形全等(键记为“边角边”或“SAS”)在△ABC和△A′B′C′中,AB=A′B′AC=A′C′∠BAC=B∠′A′C′∴△ABC≌△A′B′C′(SAS)复习如图,小明不慎把一块三角形的玻璃打碎成两块。试问:小明应该带哪一块碎片到商店去才能配一块与原来一样的三角形玻璃呢?1、想想猜猜ⅠⅡⅠⅡ解:带第Ⅱ块去。2、探索活动活动一:猜想、测量、验证观察图中的三角形:1、先观察,猜一猜哪两个三角形是全等三角形?2、哪些条件决定了△ABCFDE?≌△3、△ABC与△PQR有哪些相等的条件?为什么它们不全等?AB360°40°C340°60°PRQ60°40°DFE3已知:△ABC求作:△A/B/C/,使A/B/=AB,∠A/=A∠,∠B/=B∠。把画好的△A/B/C/剪下,放到△ABC上,它们全等吗?问:通过实验可以发现什么事实?活动二:做一做画一个△A′B′C′,使A′B′=AB,∠A′=∠A,∠B′=∠B:画A′B′=AB;在A′B′的同旁画∠DA′B′=∠A,∠EBA′=∠B,A′D,B′E交于点C′.两角及其夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”)。探究反映的规律是:基本事实在△ABC和△A′B′C′中,AB=A′B′∠A=A′∠∴△ABC≌△A′B′C′(ASA)几何语言:∠B=B′∠注意书写时条件顺序例1.如图,D在AB上,E在AC上,AB=AC,∠B=C.∠求证:AD=AE.分析:如果能证明△ACDABE,≌△就可以得出AD=AE在△ACD和△ABE中,∠A=A∠∠C=B∠AC=AB(ASA)证明:∴△ACDABE≌△∴AD=AE图例2.如图,∠1=2∠,∠3=4∠求证:BD=BCCADB1234∠1=2,∠∠3=4∠(已知)∠ABD=ABC∠在△ABD和△ABC中∠1=2∠AB=AB(公共边)∠ABD=ABC∠∴△ABDABC≌△(ASA)∴BD=CD证明:∵∴3.巩固与提高例3.如图,已知点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=C.∠求证:BD=CEABCDEO证明:在△ACD和△ABE中∠A=A∠(公共角)AC=AB∠C=B∠∴△ABEACD≌△(ASA)∴AD=AE(全等三角形的对应边相等)又∵AB=AC∴BD=CE巩固与提高1、已知:如图,点B,F,C,E在同一条直线,FB=CE,ABED,ACFD,∥∥求证:AB=DE,AC=DFDCBAEF证明:FB=CE(∵已知)∴FB+FC=CE+FC∴BC=EF∵ABED,ACFD(∥∥已知)∴∠B=E,ACB=DFE(∠∠∠两直线平行,内错角相等)在△ABC与△DEF中{BC=EF(已证)∠B=E(∠已证)∠ACB=DFE(∠已证)∴△ABCDEF(ASA)≌△∴AB=DEAC=DF(全等三角形对应边相等)巩固与提高注:•1、在证明三角形全等时,要善于把已知的条件转化为可以直接判定三角形全等的条件。如本例2。•2、证明三角形全等是证明线段相等和角相等的常用方法。2、如图,AC与BD相交于点O,则:1.图中可看出相等的是______=______.2.要证△BAODOC≌△还需要_____个条件.3.请补充条件,填写证明方案._______________________________________根据:______________________________________________根据:______________________________________________根据:_______ABDCO∠AOB∠COD2OA=OC∠AOB=COD∠OB=ODSAS∠AOB=COD∠OB=OD∠B=D∠ASA∠AOB=COD∠OA=OC∠A=C∠ASA快来解决问题吧!3、已知,如图,要测量河两岸相对的两点A、B之间的距离,可以在AB的垂线BF上取两点C、D,使BC=CD,再过点D作BF的垂线DE。使点A、C、E在一条直线上,这时测得DE的长等于AB的长,请说明道理。---------------------------------------------------------------------------------------------------------------------------------------------------------------ABCDEF--------------------------------------------------------------------------------------------------------------------------------------------------------ABCDE已知ABBD⊥,EDBD⊥,且AE交BD于C,BC=CD分析:1、寻求已知条件:2、转化为判定的条件:∠ABC=EDC=90∠O(垂直定义)BC=DC(已知条件)∠ACB=ECD(∠对顶角相等)3、得出结论:5、训练拔高4、如图OP是∠MON的角平分线,C是OP上的一点,CAOM⊥,CBON⊥,垂足分别为A、B,△AOCBOC≌△吗?为什么?OBNPMC┎┛A解:△AOCBOC≌△。∵CAOM⊥,CBON⊥。∴∠CAO=CBO=90°∠。∵OP是∠MON的平分线,∴∠AOC=BOC∠。又∵OC=OC。∴△AOCBOC≌△。(ASA)∴∠OCA=OC∠B。1.这节课你有哪些收获?2.列举已学判定的方法。3.三角形全等的判定2ASAP102练习1.2.3