复数的几何性质VIP免费

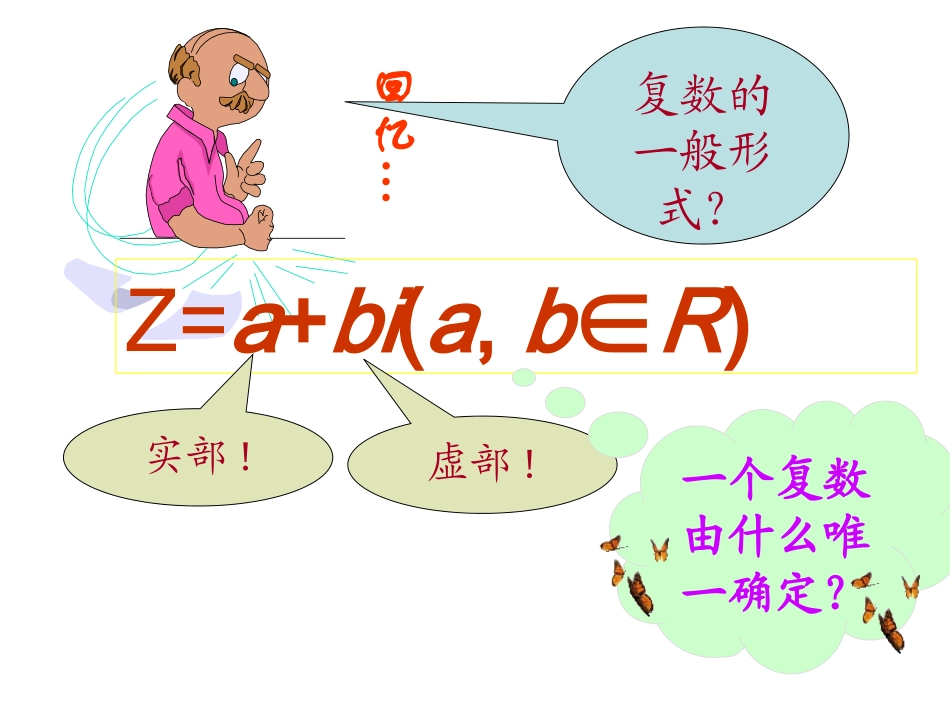
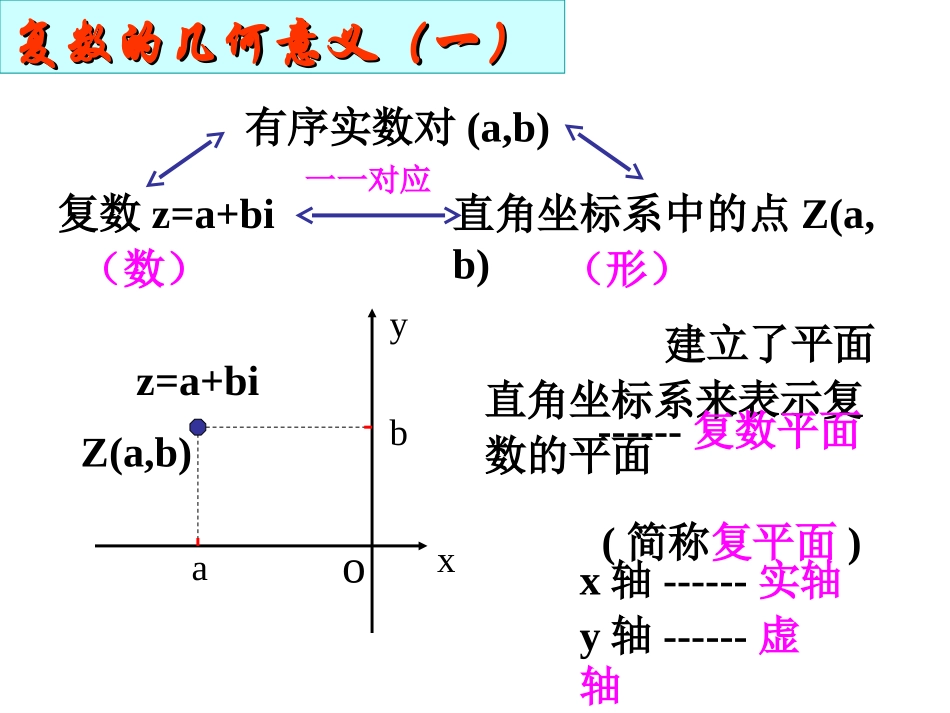
在几何上，我们用什么来表示实数?想一想？实数的几何意义实数的几何意义类比实数的表示，可以用什么来表示复数？实数可以用数轴上的点来表示。实数数轴上的点(形)(数)一一对应复数的一般形式？回忆…Z=a+bi(a,b∈R)实部!虚部!一个复数由什么唯一确定？复数z=a+bi有序实数对(a,b)直角坐标系中的点Z(a,b)xyobaZ(a,b)建立了平面直角坐标系来表示复数的平面x轴------实轴y轴------虚轴（数）（形）------复数平面(简称复平面)一一对应z=a+bi复数的几何意义（一）复数的几何意义（一）例1：在复平面内，分别用点和向量表示下列复数：4,2+i,-i,-1+3i,3-2i例2已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限，求实数m允许的取值范围。表示复数的点所在象限的问题复数的实部与虚部所满足的不等式组的问题转化(几何问题)(代数问题)一种重要的数学思想：数形结合思想020622mmmm解：由1223mmm或得)2,1()2,3(m变式一：已知复数z=(m2+m-6)+(m2+m-2)i在复平面内.证明对一切m，此复数所对应的点不可能位于第四象限。点位于第四象限，证明：若复数所对应的020622mmmm则3221mmm或即不等式解集为空集所以复数所对应的点不可能位于第四象限.小结变式二：已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点在直线x-2y+4=0上，求实数m的值。解：∵复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点是（m2+m-6，m2+m-2），∴(m2+m-6)-2(m2+m-2)+4=0，∴m=1或m=-2。复数z=a+bi直角坐标系中的点Z(a,b)一一对应平面向量OZ�一一对应一一对应复数的几何意义（二）复数的几何意义（二）xyobaZ(a,b)z=a+bi小结xOz=a+biy复数的绝对值(复数的模)的几何意义:Z(a,b)22ba对应平面向量的模||，即复数z=a+bi在复平面上对应的点Z(a,b)到原点的距离。OZ�OZ�|z|=||OZ�小结)0(12ddzz例3求下列复数的模：(1)z1=-5i(2)z2=-3+4i(3)z3=5-5i(2)满足|z|=5(z∈C)的z值有几个？思考：(1)满足|z|=5(z∈R)的z值有几个？(4)z4=1+mi(mR)(5)z∈5=4a-3ai(a<0)这些复数对应的点在复平面上构成怎样的图形？小结xyO设z=x+yi(x,y∈R)满足|z|=5(z∈C)的复数z对应的点在复平面上将构成怎样的图形？55–5–55||22yxz练习：1、已知复数Z1=3+4i，Z2=-1+5i，试比较它们模的大小。2、复平面内满足的复数z对应的点的轨迹是0432zz3、满足条件的复数z在复平面内对应点的轨迹是2iziz已知复数Z满足，则|Z|的取值范围？5|||2|izz例4：已知复数Z满足|2Z-i|=|Z-i|，求在复平面上复数Z对应的点的轨迹是什么？例5：1、如果复数Z满足|Z+i|+|Z-i|=2，那么|Z+i+1|的最小值是___________2、设复数z满足条件那么的最大值是（）（A）3（B）4（C）（D）3、在复平面上的复数Z对应于Z点，且有设则复数对应点的轨迹方程是（）（A）（B）（C）（D）4、在复平面上的复数Z=（a2-2a+4）-（a2-2a+2）i(aR)∈求复数z对应点的轨迹方程22132,1iZ,21iZ11i131i121i131i,1ziz22迁移巩固:小结:复数的几何意义是什么？复数z=a+bi直角坐标系中的点Z(a,b)一一对应平面向量OZ�一一对应一一对应复数的几何意义复数的几何意义比一比？复数还有哪些特征能和平面向量类比?做一做？作业：课本115页1、2、4二次函数的最值