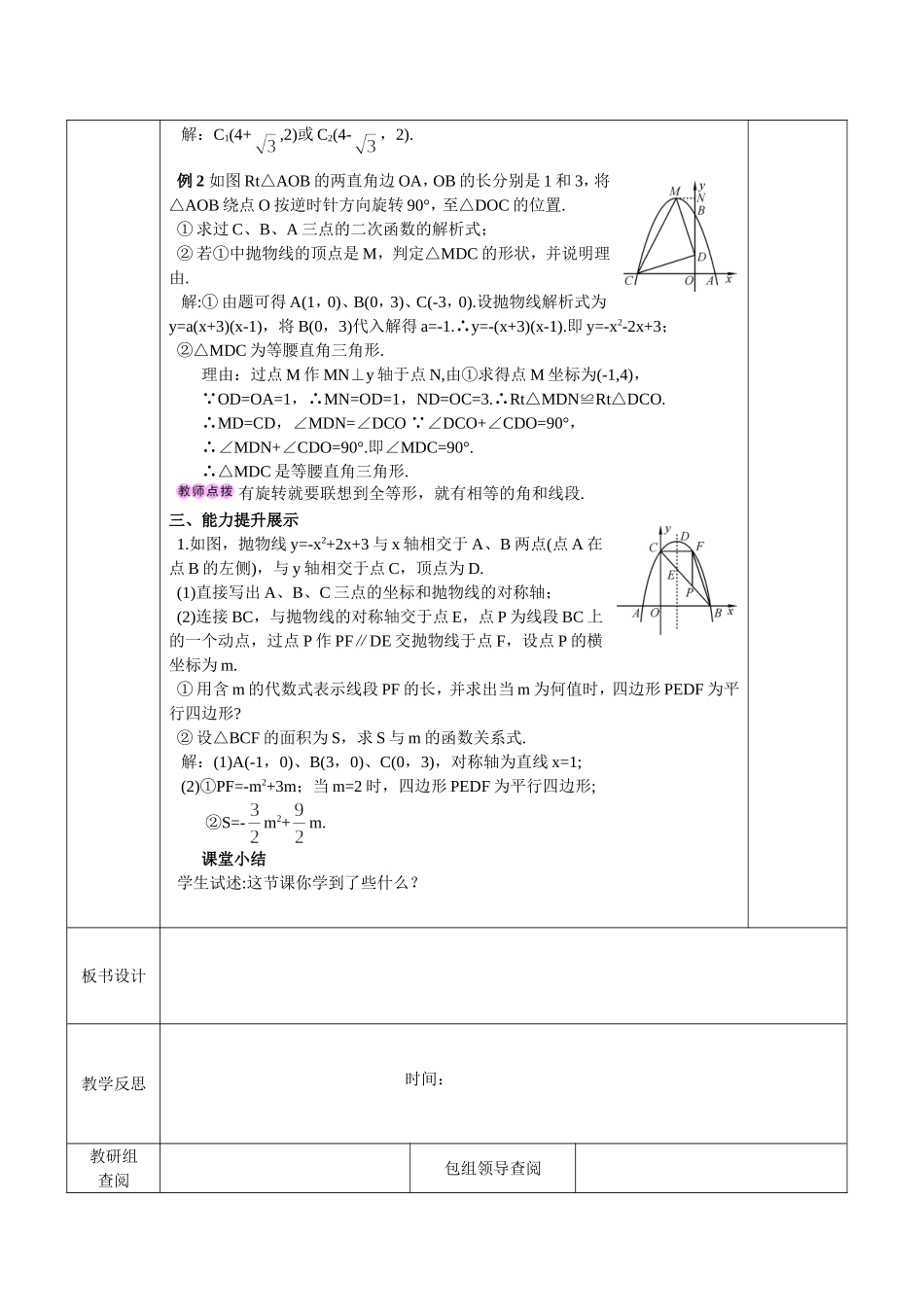
课题二次函数y=ax2+bx+c的图象与字母系数的关系总第课时课型专题课设计者龙江沙设计时间2016.11学习目标1.熟练掌握函数与方程的综合应用.2.能利用函数知识解决一些简单的实际问题.学习重点1熟练掌握函数与方程的综合应用.学习难点能利用函数知识解决一些简单的实际问题.教学流程教学过程设计意图阅读教材第43至46页,自学“问题”、“思考”与“例题”,理解二次函数与一元二次方程的关系,会判断抛物线与x轴的交点情况,会利用二次函数的图象求对应一元二次方程的近似解.一、自学检测展示例1将抛物线y=x2+2x-4向左平移2个单位,又向上平移3个单位,最后绕顶点旋转180°.①求变换后新抛物线对应的函数解析式;②若这个新抛物线的顶点横纵坐标恰为x的整系数方程x2-(4m+n)x+3m2-2n=0的两根,求m、n的值.解:①y=x2+2x-4=(x+1)2-5.由题意,可得平移旋转后抛物线的解析式为y=-x2-6x-11.②该抛物线顶点坐标为(-3,-2).设方程两根为x1,x2,则有x1+x2=4m+n=-5,x1·x2=3m2-2n=6.即解得或熟练运用二次函数平移规律解决问题,二次函数与一元二次方程的转化,以及一元二次方程根与系数的关系也是解决问题的常用之法.二、重难点突破展示1.二次函数y=ax2+bx+c的部分对应值如下表所示,二次函数y=ax2+bx+c的图象的对称轴为直线x=1,当x=2时,对应的函数值y=-8.x…-3-20135…y…70-8-9-57…2.若二次函数y=-x2+2x+k的部分图象如图,则关于x的一元二次方程-x2+2x+k=0的一个解x1=3,另一个解x2=-1.可根据抛物线的对称性.3.函数y=(x-2)(3-x)取得最大值时,x=.先化成顶点式,再确定其最大值.4.二次函数y=x2-8x+15的图象与x轴交于A、B两点,点C在该函数图象上运动,若S△ABC=2,求点C的坐标.解:C1(4+,2)或C2(4-,2).例2如图Rt△AOB的两直角边OA,OB的长分别是1和3,将△AOB绕点O按逆时针方向旋转90°,至△DOC的位置.①求过C、B、A三点的二次函数的解析式;②若①中抛物线的顶点是M,判定△MDC的形状,并说明理由.解:①由题可得A(1,0)、B(0,3)、C(-3,0).设抛物线解析式为y=a(x+3)(x-1),将B(0,3)代入解得a=-1.∴y=-(x+3)(x-1).即y=-x2-2x+3;②△MDC为等腰直角三角形.理由:过点M作MN⊥y轴于点N,由①求得点M坐标为(-1,4),∵OD=OA=1,∴MN=OD=1,ND=OC=3.∴Rt△MDN≌Rt△DCO.∴MD=CD,∠MDN=∠DCO∵∠DCO+∠CDO=90°,∴∠MDN+∠CDO=90°.即∠MDC=90°.∴△MDC是等腰直角三角形.有旋转就要联想到全等形,就有相等的角和线段.三、能力提升展示1.如图,抛物线y=-x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.(1)直接写出A、B、C三点的坐标和抛物线的对称轴;(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?②设△BCF的面积为S,求S与m的函数关系式.解:(1)A(-1,0)、B(3,0)、C(0,3),对称轴为直线x=1;(2)①PF=-m2+3m;当m=2时,四边形PEDF为平行四边形;②S=-m2+m.课堂小结学生试述:这节课你学到了些什么?板书设计教学反思时间:教研组查阅包组领导查阅